July 18, 2019 feature
Illusive patterns in math explained by ideas in physics
Patterns appear widely throughout nature and math, from the Fibonacci spirals of sea shells to the periodicity of crystals. But certain math problems can sometimes trick the human solver into seeing a pattern, but then, out of the blue, the pattern suddenly disappears. These illusive patterns crop up in many areas of math, with one example coming from certain calculus integrals that have deceived the intuition of even the best mathematicians.
Now in a new study, two physicists have approached these integrals using the physics concept of random walks. Whereas solving these integrals usually requires a great deal of effort and ingenuity, the physicists have shown that the new approach can find solutions intuitively and sometimes even without the need for explicit calculations.
Physicists Satya N. Majumdar and Emmanuel Trizac at the University of Paris-Sud, CNRS, in France, have published a paper on using random walkers to solve integrals in a recent issue of Physical Review Letters.
"We have shown that physics insight allows us to obtain in a calculation-free way a wealth of curious integrals, and in addition, to obtain previously unknown identities (either integrals, or equalities between discrete sums and integrals)," Trizac told Phys.org. "Our work reveals that when mathematical intuition is deceived, physical intuition may save the day."
Patterns in Borwein integrals
The integrals in question (see figure) are "Borwein integrals," named after David and Jonathan Borwein (father and son), who noticed unusual patterns in them in 2001. The Borwein integrals involve the product of sinc (cardinal sine) functions, which have widespread applications, such as in optics, signal processing, and other areas. These two particular integrals can be used to compute the volumes of hypercubes.
Solving the Borwein integrals involves substituting numbers in for the variable n. Each number gives a different solution value, allowing mathematicians to observe patterns in the resulting sequence of values. For example, for the first integral (In), when you substitute the numbers n = 1-7, you get the answer π every time. But when you get to n = 8, the answer is ever so slightly less than π (roughly π – 10-10). The first time mathematicians calculated this value on a computer, they thought there must be a bug in the software. But the answer was confirmed, and the subsequent terms (for n = 9, 10, etc.) keep getting ever so slightly smaller.

Some patterns persist even longer. For the second integral, Jn, the first 56 terms of the sequence (obtained by substituting the numbers 1 through 56 for n) are all π/2. But the 57th term is approximately π/2—10-110, and the subsequent terms continue to decrease. (Things can become even more extreme: For one variant of the Borwein integrals—not discussed here—a constant value pattern holds for an astounding first 10176 terms of the sequence, after which point the pattern finally breaks.)
Mathematicians can explain why these patterns suddenly break, at least in mathematical terms. Notice that both Borwein integrals above contain the function sinc(ank), where an = 1/(2n—1). If you substitute in the numbers 1, 2, 3, … for n in this expression, you get the sequence 1, 1/3, 1/5, 1/7, 1/9, ... . The Borweins noticed that the first term, 1, is not only larger than all of the other terms that come after, but it's even larger than the sum of the next few terms—the second through seventh terms, to be exact, as 1/3 + 1/5 + 1/7 + 1/9 + 1/11 + 1/13 = 0.955… , which is less than 1. But when adding the eighth term, 1/15, to this sum, the answer is 1.02…, so just above 1. It turns out that it's no coincidence that the seventh term is the last term for which the integral evaluates to π, and the eighth term is the point at which the pattern breaks.
The Borweins proved a theorem (see figure) that states this idea in more general terms. The theorem holds for the second integral, Jn, as well. Accounting for the cosine function in Jn changes the expression above to 2/(2n—1), due to the property cos(a)sinc(a) = sinc(2a), so that the first term is 2 instead of 1. As the sum of the second through 56th terms of the expression is less than 2, but adding the 57th term pushes the sum over 2, the theorem holds.
Random walkers
Although the theorem helps to explain when the Borwein integrals' temporary patterns break, it is still not completely clear why the theorem holds in the first place.
In the new paper, Majumdar and Trizac have offered some physical intuition into the theorem by connecting it to some well-understood concepts in probability theory and statistical mechanics. They noticed that the integral in the theorem has close ties to the uniform probability distribution, which is widely used throughout science. Specifically, the Fourier transform of the uniform probability distribution happens to be just the sinc function, which yields the Borwein integral for n = 1. This connection bridges the Borwein integrals to the physical world, so that by using relevant parameters, events that follow a uniform distribution can be used to model the sequence of solutions to the Borwein integrals.
To describe this connection in a more physical context, the researchers looked at random walkers. A random walker is an abstract object that can move a certain distance in any direction, where the exact distance is chosen randomly from a continuous interval of values, and each of these values is equally likely to be chosen (i.e., it follows a uniform distribution). Random walkers can accurately model a variety of random phenomena, such as stock market prices, the paths of foraging animals, and the paths of molecules in a gas, which occur in one, two, or three dimensions, respectively.
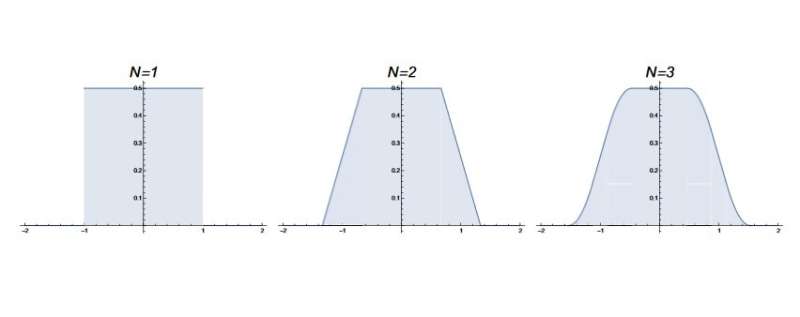
In the new paper, the physicists show that the movements of infinitely many random walkers can be used to model the emergence and disappearance of the patterns in the Borwein integrals. To begin, the random walkers all start at the point zero on the one-dimensional number line. For the first step, each walker is allowed to move a random distance of up to 1 unit, either left or right. For the second step, each walker may move a random distance of up to 1/3, then a random distance of up to 1/5, then 1/7, 1/9, etc. That is, each successive allowable step distance corresponds to the next value of the expression 1/(2n—1).
The main question is, what is the fraction of random walkers at the starting point (the origin) after each time step? It turns out that the fraction (more precisely, the probability density) of walkers at the origin at each time step n corresponds to the solution to the Borwein integral using the same n value.
As the physicists explain, for the first seven steps, the probability density that a walker ends up at the origin is always ½, which via the theorem above corresponds to an integral value of π. The key idea is that, up to this time, the density of walkers at the origin is the same as if the entire number line was uniformly populated with walkers. In reality, as the maximum distance of each step is restricted, only part of the number line is accessible, i.e., the walkers' world is finite.
However, for the first seven steps, the walkers at the origin perceive that their world is infinite, since they do not possess any information about the existence of boundaries that would indicate that the world is finite. This is because none of those walkers that reached the outer boundary of their world (+1 or -1 after the first step) would have been able to make it back to the starting point in less than seven steps, even if taking the maximum size steps allowed and all in the direction toward the starting point. As these walkers had zero probability of showing up at the starting point before the eighth step, they could not affect the fraction of random walkers at the starting point. So for the first seven steps, the density of walkers at the origin is fixed at ½ (it is "protected").
But once those walkers that have reached +1 or -1 return to the origin, the situation changes. After the eighth step, it's possible that some of these walkers return to the starting point. Now these walkers act as "messengers" in the sense that their return to the starting point reveals the existence of a boundary, telling the other walkers at the origin that their world is finite, and therefore influencing the density of walkers at the origin.
Since these messenger walkers made it back to the starting point, it becomes clear that some other boundary-reaching walkers did not make it back, but instead may have kept continuing to move further away. As a result, the probability distribution becomes more spread out, causing the fraction of walkers at the origin to gradually erode from ½ (or π for the integral). It is this erosion that explains why the values of the first Borwein integral decrease ever so slightly for n ≥ 8. A similar argument holds for the second Borwein integral (see video).
By connecting the Borwein integrals to the probabilities of random walkers, the new results offer a completely different approach to solving these integrals than through direct calculation. The physicists showed that the same approach can be applied to many other integrals in addition to the two described here, including extensions to higher dimensions. The researchers expect that the approach has the potential to provide calculation-free solutions to many other integrals that are otherwise very difficult to solve.
"Random walk problems and their infinite ramifications form one of the cornerstones of modern physics with a wide range of applications in physics, chemistry, biology, engineering, etc.," Trizac said. "Since our derivation of intriguing integrals involves basic concepts from random walk theory, we expect that new identities and integrals, with real-world applications, may be derived using our key idea in the near future."
More information: Satya N. Majumdar et al. When Random Walkers Help Solving Intriguing Integrals, Physical Review Letters (2019). DOI: 10.1103/PhysRevLett.123.020201
Journal information: Physical Review Letters
© 2019 Science X Network



















