On-chip mechanical exceptional points based on an optomechanical zipper cavity

Exceptional points are a distinct type of spectral singularity in non-Hermitian systems and their intriguing physics are in study with optical exceptional points. Exceptional points are singularities in the energy functions of a physical system, where two light modes can coalesce to produce unusual effects. Mechanical oscillators are a system beyond photonics that can couple with many physical systems to further explore within mechanical sensing, topology energy transfer and non-reciprocal dynamics.

In a new study now available in Science Advances, Ning Wu and a team of scientists in electronic engineering, science and technology in China developed on-chip mechanical exceptional points with a silicon optomechanical zipper cavity. During the process, they coupled two near-degenerate mechanical breathing modes via a single colocalized optical mode. The team tailored the dissipative and coherent couplings between the two mechanical oscillators to observe a distinct feature of exceptional points. The outcomes provide a fundamental platform to investigate the physics behind the mechanical exceptional points on silicon chips with possible applications for hyper-sensitive measurements.

Non-Hermitian physics

Non-Hermitian systems exchange energy with the outside environment quite differently from conservative Hermitian systems. Exceptional points exist within non-Hermitian systems and are observed as special degenerate points of spectra. Because of their exotic nature, researchers expect intriguing physics concepts from the phenomenon. In the past, optical exceptional points had shown their potential across optics and microwave cavities, photonic crystal slabs and multilayered plasmonic structures.

Researchers have also observed counter-intuitive phenomena experimentally. For example, if a small disturbance of specific strength acted on the exceptional points, the spectral splitting observed was proportional to the strength of interest. The exceptional points in other physical systems can be further explored similarly.

During this work, Wu and colleagues demonstrated on-chip mechanical exceptional points in an optomechanical zipper cavity at an ambient environment. The scientists coupled two near-degenerate gigahertz mechanical breathing modes using a singular optical mode. The outcomes pave the way to conduct high sensitivity measurements with mechanical exceptional points integrated on the platforms to ultimately set the stage to study the physics underlying such phenomena.

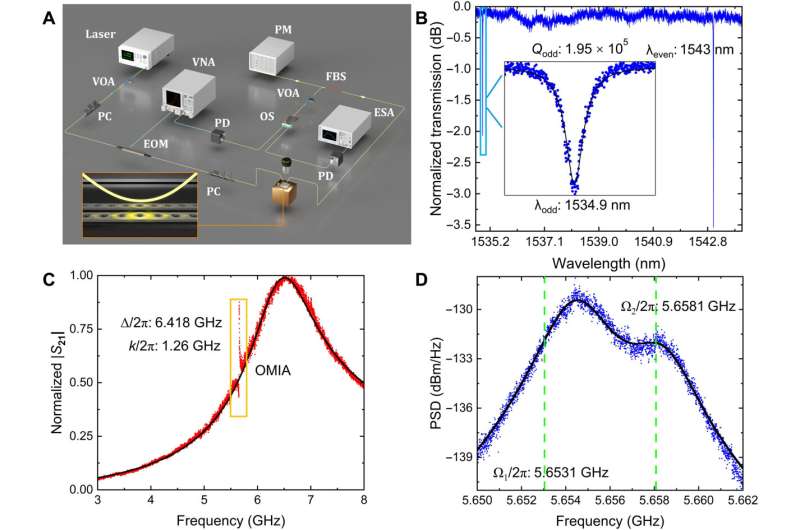
Mechanical exceptional points

Mechanical exceptional points are based on multimode optomechanical coupling; the phenomenon occurs as two independent pendulums with different oscillations, interacting with an optical mode. The optical mode facilitates a bridge-like connection between the two mechanical modes to regulate the coupling strength between the two.

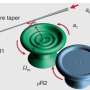
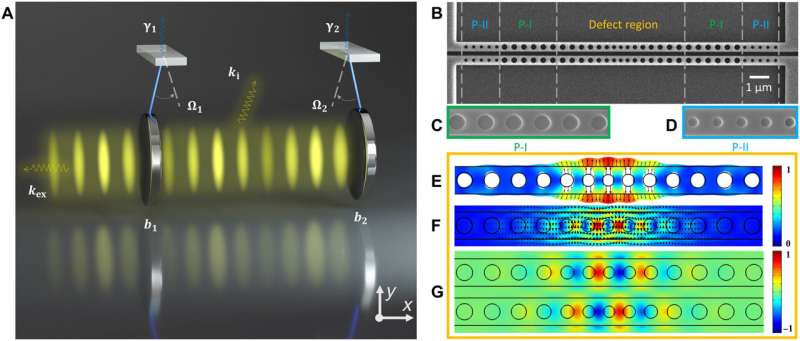
Based on the features of a multimode optomechanical coupling model, the researchers proposed and designed an optomechanical zipper cavity containing two identical silicon nanobeam cavities with a nano-scale gap between them. The researchers generated the cavity on a silicon-on-insulator wafer and used a pump-probe scheme to monitor the detuning and optical dissipation rate. They excited the optical odd mode to realize the mechanical exceptional points with a resulting Lorentzian fitting.

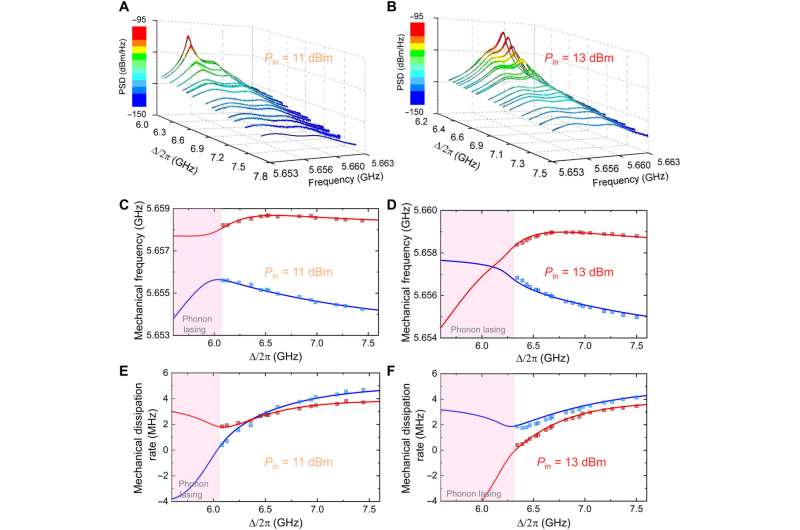
The evolution of the eigenvalue

Wu nd the team analyzed the evolution of the eigenvalue of the mechanical modes by scanning the optical detuning gradient at a fixed laser power. The team noted the occurrence of phonon lasing in both the lower-frequency mode and higher frequency mode at separate instances as evidence of coupling between the two mechanical oscillators. The physicists next obtained the mechanical eigenvalues from the mechanical spectra to observe its evolution; the experimental data were consistent with the theoretical values.

Based on the outcomes, the researchers continued to reconstruct the topological surface of the mechanical eigenvalues at different laser powers and detuning values to next focus on the variation of eigenvalues near the exceptional points.

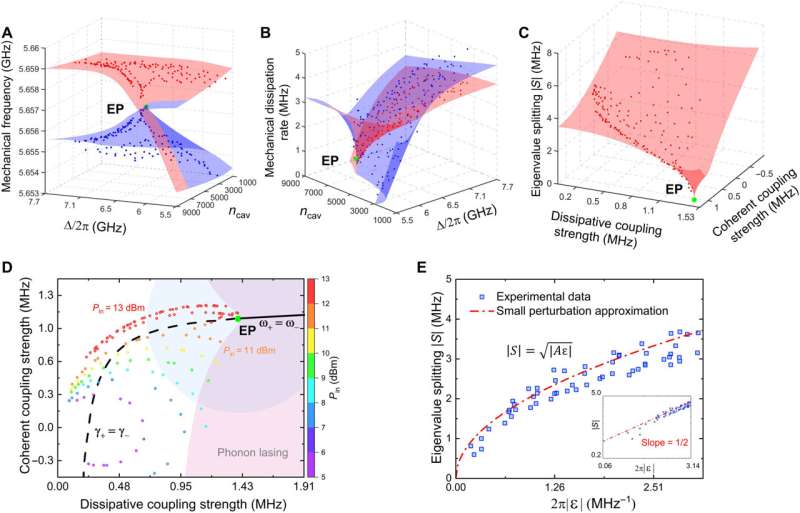
Outlook

In this way, Ning Wu and colleagues developed an experimental setup and noted a larger difference of mechanical frequency for enhanced frequency splitting near the exceptional points. They used a blue-detuned laser to reduce the mechanical linewidth while maintaining a self-reference detection scheme of frequency splitting on the device to enable a robust system for mechanical frequency drifts. The device could therefore realize high-sensitivity sensors combined with anti-damping modes and mechanical exceptional points.

The outcomes offer a reliable, integrated platform to comprehensively study and integrate non-Hermitian physics. The scientists envision using the red detecting laser to investigate multimode optomechanical cooling and nonreciprocal dynamics of the mechanical exceptional points. The new research outcomes can also lead to understand both higher-order exceptional points and multimode dynamics in the phonon laser regime on the same platform.

© 2023 Science X Network