New model describes puffs, slugs and the role of randomness in transitional turbulence
Mention the word "turbulence" and you might conjure up images of bumpy flights, stormy weather, and choppy ocean or river currents. For many, turbulence is a fact of daily life, yet it is also one of the most poorly understood physical phenomena. In particular, the point at which a fluid's motion transitions from smooth and predictable flow (known as "laminar") to random and unpredictable (known as "turbulence")—the so-called laminar-turbulent transition—continues to puzzle scientists since Osborne Reynolds first experimentally studied it in pipes in 1883.
Now, a team of scientists based at the University of Illinois Urbana-Champaign, the University of California San Diego, and Academia Sinica in Taiwan have shown how to account for the random patterns and dynamics of turbulence in pipes in the transitional regime. Their work uses novel ideas that originate in such disparate fields as statistical mechanics and ecology and it builds on the growing evidence that the laminar-turbulent transition has statistical properties that can best be thought of in terms of the theory of non-equilibrium phase transitions.
The team comprises UIUC physics graduate student Xueying Wang, Academia Sinica researcher Hong-Yan Shih, and UIUC Swanlund Endowed Chair Emeritus of Physics and Research Professor Nigel Goldenfeld. Goldenfeld is currently the Chancellors' Distinguished Professor of Physics at the University of California San Diego.
The authors published their results on July 11th, 2022, in the journal Physical Review Letters.
Puffs and slugs are features of transitional turbulence
Reynolds discovered that in pipes, the laminar-turbulent transition occurs in a patchy way as the flow speed is increased. Blobs of turbulent fluid, known today as "puffs," appear near the laminar-turbulent transition, and are separated by regions of laminar flow. The precise ways in which the puffs appear and move or even split into two depend on the geometry of the space through which a fluid flows. These complex phenomena contribute to turbulence's well-earned reputation as one of the last outstanding problems in classical physics. At even higher speeds, turbulent patches actually grow rather than just move around or split: these growing regions of turbulence are called "slugs."
To build a clearer picture of the transition to turbulence, the researchers developed a new minimal model to understand puffs and slugs using methods imported from theoretical population biology. The researchers found that they could represent the fluid's energy flow near the laminar-turbulent transition in terms of the energy flow that arises in a predator-prey ecosystem, in which nutrients are the energy of the background flow, the predator is a certain flow structure that inhibits turbulence, and turbulence is the prey. This ecological model recapitulates turbulent behavior in both pipe and Taylor-Couette flow, a type of rotational flow—a goal that previous models failed to achieve.
Goldenfeld says, "Six years ago, a breakthrough was made with theoretical and experimental evidence converging on a description of turbulent puffs emerging from laminar flow, in terms of phase transition theory. However, that work left open the question of what happens at higher flow speeds away from the tipping point itself.
"Our new work shows that the same conceptual framework and methods also apply in the slug regime and recapitulate in remarkable detail the experimental findings. It is fantastic to see concepts from phase transition theory and ecology come together in the completely different problem of fluid mechanics."
Slugs themselves exhibit interesting behaviors and come in two flavors, weak slugs and strong slugs, both of which are characterized by at least one "front," a region containing a boundary between laminar and turbulent fluids.
Lead author Wang explains, "The front of a slug is like a weather front. On one side of the front is laminar fluid. On the other side is turbulence. The front is like a phase boundary, and it moves in space at a steady speed. In pipes you get slugs as well as puffs. But weak slugs at lower fluid speed have only one front upstream, whereas strong slugs at higher speed have fronts in both the upstream and downstream directions. These factors and the richness of transitional phenomena make understanding transitional turbulence really hard. Our work provides a unified framework that handles all these regimes, different flow geometries, and the inherent randomness."
Predator-prey models and turbulence converge
The researchers were able to take advantage of a surprising connection they had found in previous work between population biology and transitional turbulence.
Modeling how predators interact with their prey is a popular theme in population biology. The basic idea is straightforward: predators reproduce and eat prey, reducing their population; prey also reproduce, restoring their numbers and providing predators with food. Then the cycle repeats. Simply put, predators inhibit prey, while prey reinforce predators. Scientists can deduce much information from these models, such as how predator and prey populations vary over time, as well as how long it takes for each to die out caused by, say, a lack of food or over-predation.
In an earlier study, Shih and Goldenfeld, working with former undergraduate Tsung-Lin Hsieh (now a postdoctoral fellow at Princeton University), showed that there exists an analogy between predator-prey models and turbulence that can be cast in mathematical terms. When fluid flows through a pipe, two types of fluid motion are generated. The first type is a vortex pattern swirling around the axis of the pipe, called "zonal flow." The second type is turbulence along the pipe axis. The authors found that turbulence accumulates steadily and activates zonal flow, which subsequently suppresses turbulence. In other words, zonal flow corresponds to predators and turbulence corresponds to prey.
The researchers found that the probability distribution of the lifetime of transitional turbulence precisely matched that of predators and prey in an ecosystem, a stunning connection considering that population biology and fluid dynamics are seemingly disparate fields.
Hong-Yan Shih comments, "This connection helps us understand the complex transitional behavior of turbulence from the point of view of phase transitions in statistical mechanics. Specifically, this discovery provides the key ingredients to construct an effective theory, which leads to the prediction that the laminar-turbulent transition in fluids is a non-equilibrium phase transition in the directed percolation universality class.
"Directed percolation can be thought of as the familiar process that happens when water drips through coffee grounds in a percolator. If the grounds are too tightly packed, water can't get through. On the other hand, if the grounds are too loosely packed, water can get through but the coffee is undrinkable. There's a critical point where the water just manages to get through and takes long enough so that the coffee tastes good.
"Mathematically, that phenomenon is exactly what happens in the transition to turbulence and the transition of a functioning ecosystem. The mathematics of phase transitions, founded in the Nobel Prize–winning work of K. Wilson, explains how this remarkable phenomenon arises."
This prior work, however, looked at the turbulence of a single puff. Real life isn't as simple, and real fluids near the laminar-turbulent transition contain multiple puffs that grow, die out, and interact in complex ways as the flow speed increases. The researchers needed to extend their model to capture more complicated dynamics beyond those of a single puff.
Extending the predator-prey model by incorporating nutrients
To capture the complex dynamics found in experiments beyond the critical point in the current study, the authors decided to take into account energy balance in pipe flow.
Wang explains, "Turbulence is a dissipative structure that needs constant energy input to be sustained, and that energy comes from the laminar flow. This fact was previously shown by exact computer simulations of the fluid equations, but did not allow us to understand in a predictive way the phenomena that would emerge."
The researchers realized that, just like zonal flow and turbulence require energy to persist, predators and prey need nutrients from their environment to survive.
"We wanted to make a minimal model of the full energy balance to extend the previous work and capture energy extraction of turbulence from laminar mean flow," Wang adds. "So we introduced another component into the 'ecosystem': nutrients, which represent the kinetic energy of the mean flow."
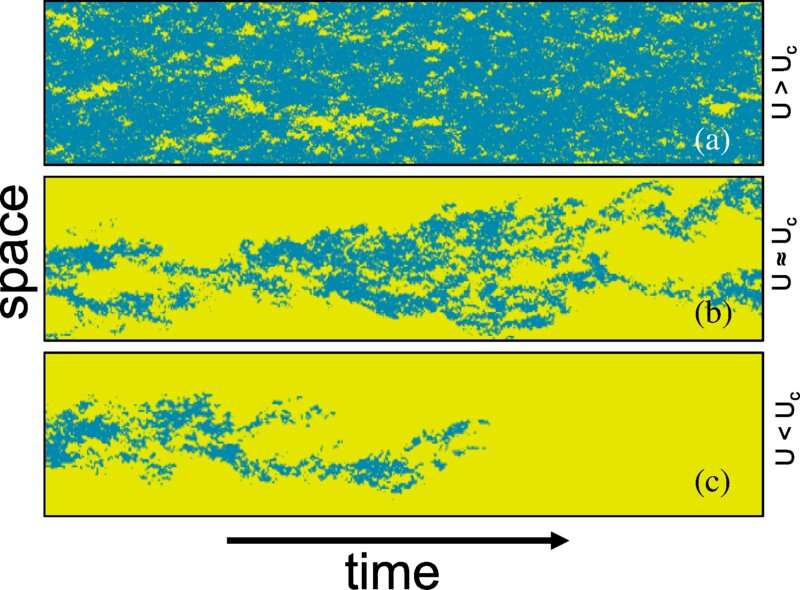
The researchers numerically simulated the extended predator-prey model on a two-dimensional lattice having a length much larger than its width. They watched what happens when nutrients—that is, laminar state energy, from the fluid dynamics perspective—flow into the ecosystem, are consumed by the turbulence, and are restored downstream of the turbulence.
The model maps several pathways for energy and population dynamics. The first pathway takes input energy from the energy budget to turbulent energy, like prey extracting nutrients from their environment. A second pathway takes turbulent energy to zonal flow energy, like predators eating prey.
Once they established these predator-prey-inspired pathways, they sat back and watched computer simulations based on the new model, wherein energy entered the pipe and passed through the pathways randomly. Out of the randomness emerged features of transitional turbulence such as puffs, slugs, and their associated fronts, reproducing results seen in experiments. The simulations showed that the appearance of puffs or slugs—and whether slugs are of the weak or strong type—is determined by the input energy (or equivalently, the speed) of the fluid flow.
The researchers then successfully reproduced all the transitional phenomena observed in pipe flow experiments and explained the underlying physics of puff splitting and growth. Specifically, they found that puff splitting and interaction is highly probabilistic. As the fluid speed increases, the probability of puff splitting also increases. The puff-slug transition is gradual, and it occurs when puffs split so frequently that they start to fill up the system densely.
Rotational flow and new questions for turbulence
In addition to pipe flow, the researchers also simulated a special type of rotational flow known as Taylor-Couette flow in which a fluid moves in the space between two concentric cylinders and the outer cylinder rotates relative to the inner one. Unlike pipe flow, where the energy enters from the high-pressure end of the pipe, Taylor-Couette flow is sustained by shear, the stress that occurs when two boundaries move parallel to one another. The new model easily incorporated this difference and reproduced the patterns of transitional turbulence seen in experiments, demonstrating the flexibility of the model.
"We showed that the rich and complicated dynamical features in transitional pipe flow can be understood with a simple three-level stochastic predator-prey model based on energy balance in pipe flow," says Wang. "Our model also works for quasi-one-dimensional Taylor-Couette flow. Since energy balance generally holds in fluid systems, we expect our model to be applicable to systems with more complicated geometries as well."
Having described turbulence broadly by implementing their model in two different geometries, the team is already looking to answer new questions.
Goldenfeld says, "The next challenge is to see if and how our probabilistic model can be extended to two- or three-dimensional flows. This problem has been intensely studied for well over twenty years, with new experimental data starting to appear."
For his part, Goldenfeld is pleased to see diverse techniques converge to solve problems in complementary ways, a beautiful demonstration of how different fields of science can inform each other.
Goldenfeld summarizes, "Our results show how stochastic dynamics, pattern formation, phase transitions, and modeling concepts from diverse fields such as ecology can bring new tools, predictions, and insights into a problem previously considered within the more narrow disciplinary focus of fluid dynamics. It is exciting to see how successful minimal modeling is at capturing complex physical phenomena in a quantitative way."
More information: Xueying Wang et al, Stochastic Model for Quasi-One-Dimensional Transitional Turbulence with Streamwise Shear Interactions, Physical Review Letters (2022). DOI: 10.1103/PhysRevLett.129.034501
Journal information: Physical Review Letters