What does turbulence have in common with an epidemic?

Fluid flows can take one of two forms: well-ordered "laminar" or highly disordered "turbulent" motion. Although everyday experience shows that laminar motion in simple shear flows as in pipes or channels gives way to turbulence as the flow speed increases, the exact nature of this transition has remained a riddle since its first study in the 19th century.
IST Austria professor Björn Hof and his colleagues from the Max Planck Institute for Dynamics and Self-Organization in Göttingen and the Friedrich-Alexander-University Erlangen-Nürnberg have considerably contributed to answering this question in the past. In their recent publication—in Nature Physics in February 2016—they were eventually able to show that the transformation can be fully characterized as a phase transition, based on their study of the so called "Couette flow". This kind of flow consists of a viscous fluid that is confined between two parallel walls that move in opposite directions.
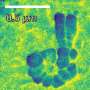
Just like in pipes or channels, turbulence in Couette flow first appears in localized domains and seems to co-exist happily with laminar regions. Investigations over exceedingly long times, however, reveal that turbulent and laminar regions in reality compete and try to annihilate each other. Below a critical speed, the laminar phase wins, but yields to turbulence beyond some threshold, resulting in an ever changing co-existence pattern of laminar and turbulent domains.
A qualitatively similar behavior is known from "directed percolation". This simple statistical physics model is believed to describe many contact processes in nature such as the spreading of forest fires or of an epidemic in a population. Surprisingly, all these very different phenomena should be characterized by the same three numbers at the transition point. These three "critical exponents" fully describe the resulting fluctuating co-existence patterns for this type of phase transition.
The turbulent Couette experiments could precisely confirm predicted critical exponents. Apart from finally providing an answer for the nature of the onset of turbulence, they are also one of the first experimental confirmations of the directed percolation universality class. Hof comments: "We believe that the start of sustained turbulence in other shear flows will equally fall into the directed percolation class which future research will need to verify."
More information: Directed percolation phase transition to sustained turbulence in Couette flow, Nature Physics, DOI: 10.1038/nphys3675
Journal information: Nature Physics
Provided by Institute of Science and Technology Austria