Climate tipping might be predicted using algebraic topology

The Earth's climate system seems to have shifted abruptly between colder and warmer modes in the past. Do we risk the same today from anthropogenic climate change? Frankly, climate models cannot answer that question yet. But a result in the journal Chaos by Gisela D. Charó, Mickaël D. Chekroun, Denisse Sciamarella and Michael Ghil suggests a way to resolve the matter. Analyzing a model that combines the two leading theories for climate change with algebraic topology tools, the authors show that the climate system indeed progresses through abrupt transitions, also known as tipping points. These tools are applicable to reduced climate models and they well might help assess whether the Earth's climate system on a whole is about to tip due to global warming. The work is part of the TiPES project, a European science collaboration on tipping points in the Earth system.
How does the climate evolve?
"It is one of the truly unsolved mysteries about the climate sciences that we are trying to get at," explains Michael Ghil, École Normale Supérieure, Paris, France.
There have been essentially two complementary views of what makes climate evolve. One is the deterministically chaotic view of Edward Lorenz. This is the chaos theory that is widely known through the idea that a butterfly flapping its wings on one continent can be the origin of a raging storm on another continent.
The other view is that of Klaus Hasselmann, the recent Nobel Prize winner, who said the climate system is stochastic and everything fluctuates but regresses to the mean.
The combination looks strange
"We have earlier, in 2008, brought these two theories together and shown that things get a lot more interesting if you have both deterministic chaos and stochastic perturbations," says Michael Ghil.
The result from 2008, a so-called random attractor, can be seen in this video.
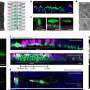
This random attractor changes with time. The shape it takes at a given instant, called a snapshot, determines where the climate system is most likely to be. It has not been clear, however, how to interpret the random attractor's changes in time. What does its changing path mean for our understanding of the climate? Algebraic topology now helps with that.
Abrupt changes
Algebraic topology is quite abstract but its results are easy to understand. If two systems' geometric objects are qualitatively similar, they contain the same number of holes.
The analysis in Chaos of the climate's random attractor reveals that over time, holes appear and disappear. This means the system shifts between different regimes. The transitions seem to be instantaneous. And because the analysis in effect reveals changes in the most fundamental properties of the physical system being analyzed, the results suggest that the nature of Earth's climate indeed is to evolve through abrupt transitions—commonly known as tipping points.
Early warning
The method might have implications for predicting an eventual tipping of the climate system. Today, such a tipping of the entire climate system is much too complicated an occurrence to establish an early warning system for. However, algebraic topology could be the answer.
"This is a fairly robust method of establishing critical conditions in very complex situations. So I think that it should be possible to use these tools in order to really foreshadow transitions in a system that is as complex as the climate system," says Michael Ghil.
Success in carrying out this program, however, will depend on whether climate models can be reduced to manageable sizes for analysis with the algebraic topology tools used in this work.
More information: Gisela D. Charó et al, Noise-driven topological changes in chaotic dynamics, Chaos: An Interdisciplinary Journal of Nonlinear Science (2021). DOI: 10.1063/5.0059461
Journal information: Chaos
Provided by University of Copenhagen