April 7, 2021 feature
Gate-controlled ground state crossover in a two-dimensional superconductor
In the paired fermion systems, the Bardeen-Cooper-Schrieffer (BCS) superfluidity and Bose-Einstein condensation (BEC) are two extreme limits of the ground state. In a new report in Science, Yuji Nakagawa and a team of scientists in applied physics, quantum electronics, emergent matter science and materials research in Japan, reported crossover behavior from the BCS limit to the BEC limit by varying the carrier density in a 2D superconductor electron-doped, layered material ZrNCl containing intercalated layered nitride. The team showed how the ratio of the superconducting transition temperature and Fermi temperature in the low carrier density limit was consistent with the theoretical upper bound expected in the BCS-BEC crossover regime. The results indicated how the gate-doped semiconductor provided an ideal platform for the 2D BCS-BEC crossover without additional complexities as those noted in other solid-state systems.
The BCS-BEC crossover
The phenomenon of fermion pairing, and condensation are fundamental to a variety of systems including neuron stars to superconductors and ultracold atomic gases. Two limiting cases for fermion condensation are described by two distinct theories known as the Bardeen-Cooper-Schrieffer (BCS) theory for which physicist John Bardeen et al. received the Nobel prize in 1972, and the Bose-Einstein condensation (BEC) developed by physicists Satyendra Nath Bose and Albert Einstein in 1924. The BCS theory details the superfluidity in the weak-coupling or high-density limit where individual fermions directly condense to a coherent state of fermion pairs - a type of condensation typically observed in the superconductivity of electrons. The latter often occurred during the strong-coupling, low-density limit. At first, fermion pairs behave as bosons and then they undergo the BEC to the superfluid state in a phenomenon seen in fermionic gases. The two limits are connected continuously through an intermediate regime known as the BCS-BEC crossover.
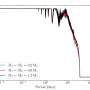
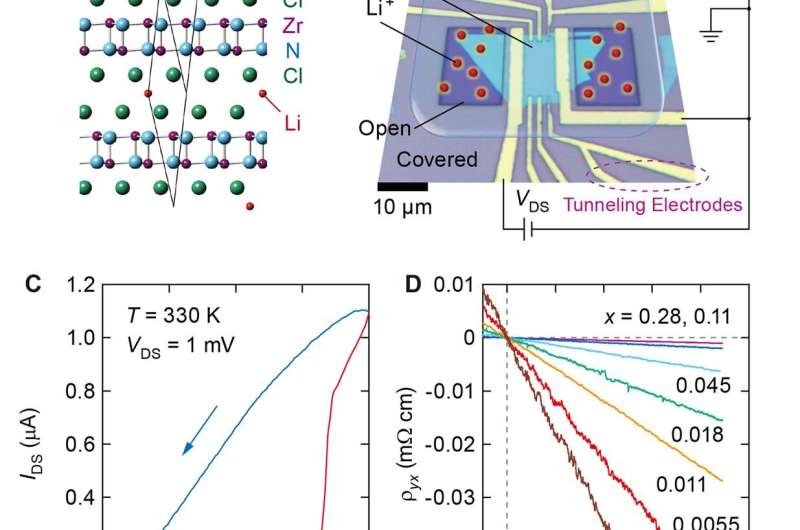
![Transport properties of LixZrNCl. (A) Temperature dependence of resistivity at different doping levels. The resistivities at x = 0.080 and 0.13 are multiplied by 5 and 10, respectively. (B) Resistivity normalized at 30 K. Each curve is shifted by 0.5, and gray dashed lines indicate zero lines. (C) Resistivity at x = 0.011 showing the BKT transition. The black line is the fit to the Halperin-Nelson formula. Inset: resistivity plotted on a [d(ln ρ)/dT]–2/3 scale. (D) Out-of-plane upper critical field Hc2 as a function of temperature. Dashed lines are linear extrapolations to 0 K for each doping levels. (E) Doping dependence of Hc2 at 0 K in (D) (top) and in-plane coherence length ξ (bottom). Credit: Science, doi: 10.1126/science.abb9860 Gate-controlled ground state crossover in a two-dimensional superconductor](https://scx1.b-cdn.net/csz/news/800a/2021/1-gatecontroll.jpg)
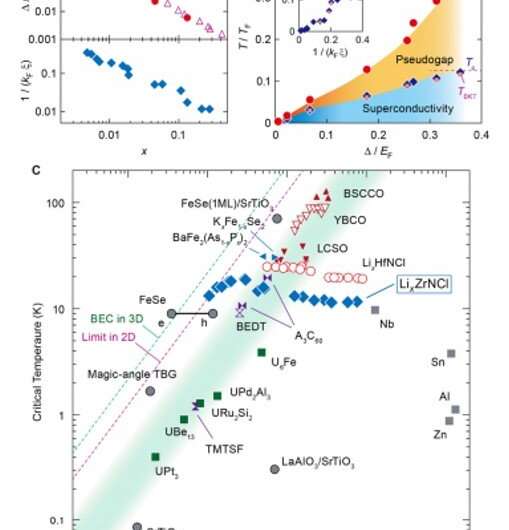
Physicists use ultracold atomic gases and superconductors as favorable experimental settings to observe the BCS-BEC crossover by controlling the coupling strength between the constituent fermions in a quasi-continuous manner. In ultracold atomic gasses the coupling strength can be highly modulated using Feshbach resonances sweeping across the crossover regime from the BEC limit. Researchers can control the carrier density and the coupling strength to enter the crossover regime from the BCS limit within superconductors. In superconductors, the dimensionless coupling strength can be determined using the superconducting gap and Fermi energy measured from the bottom of the conduction band. As the ratio between the superconducting gap and the Fermi energy increased via enhanced pairing interactions or reduced carrier density, the system entered the BCS-BEC crossover regime, accompanied by enhanced ratios of superconducting critical temperature and Fermi temperature. For example, niobium (Nb) and aluminum (Al) reside deeply within the BCS limit, while more exotic superconductors including iron-based semiconductors are located close to the BCS-BEC crossover regime. The coupling strengths are however not high enough to reach the BEC limit beyond the crossover regime due to complex activities such as low carrier density, strong electron correlation effects and magnetic ordering that cloud the phenomena. As a result, physicists remain to clearly demonstrate the BCS-BEC crossover during the study of superconductors. In this work, Nakagawa et al. studied the superconductor LixZrNCl – a lithium intercalated layered nitride to understand the phenomena.
Investigating the superconductor
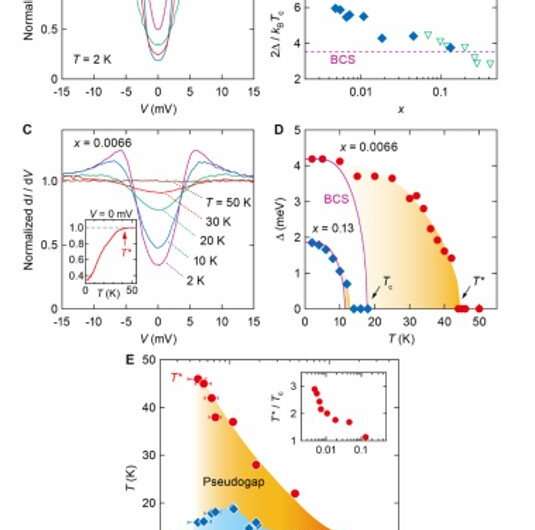
In the LixZrNCl superconductor, lithium supplied electrons to the double honeycomb ZrN layer, which formed a band insulator in the absence of doping. Researchers had previously conducted single-crystal measurements of pristine ZrNCl using ionic gating methods. In recent work, Nakagawa et al. introduced a modified device structure and noted a dimensional crossover from anisotropic three-dimensional (3D) to 2D superconductors by decreasing the carrier density. In this work, the team detailed the superconductivity behavior of LixZrNCl in an even lower carrier density regime. The scientists used an ionic-gating device structure and prepared narrow electrodes for tunneling spectroscopy on the channel region between the source and drain electrodes and covered the device with a poly (methyl methacrylate) (PMMA) resist. During gate voltage (VG) applications, the team traced the intercalation process through the measurement of source-drain current. The resistive transition in the highly doped regime was sharp, while it substantially broadened in the lightly doped regime to represent a dimensional crossover from anisotropic 3D to 2D superconductors.
The dimensional crossover
The 3D to 2D dimensional crossover of the superconductor occurred due to reduced carrier density to therefore form a unique and unexpected phenomenon to enable the crossover. The team credited the feature to the rhombohedral stacking of ZrNCl layers, where the unit contained three layers. Using density functional theory calculations, they confirmed the experimental outcomes. During the cooling process, the scientists performed tunneling spectroscopy, where the decreasing carrier density corresponded to stronger coupling. Nakagawa et al. also discussed the pseudo-gap states in several materials and compared them with the present system. The LixZrNCl material offered a simpler test bed since its band-insulator was free from electron correlation effects, magnetic orders and density waves. The team credited the pseudo gap state observed in LixZrNCl to pre-formed pair formation during the BCS-BEC crossover phenomenon. They then highlighted a bulk study, where NMR measurements on polycrystalline LixZrNCl samples showed a pseudogap state on the high doping side of the superconducting dome.
Outlook
In this way, Yuji Nakagawa and colleagues showed 2D BCS-BEC crossover by systematically tuning the coupling strength of superconductors in LixZrNCl samples. The team realized the 2D BCS-BEC crossover due to the dimensional crossover from the anisotropic 3D to 2D by reducing the carrier density of the samples. They compared this crossover to arrays of 2D clouds of Fermi gases, wherein too dimensionality was affected by the coupling strength. Additional studies on the phenomenon will help advance the understanding of fermion condensation physics.
More information:
1. Nagakawa, Y. et al. Gate-controlled BCS-BEC crossover in a two-dimensional superconductor, Science, 10.1126/science.abb9860
2. Greiner M. et al. Emergence of a molecular Bose-Einstein condensate from a Fermi gas. Nature, DOI: 10.1038/nature02199.
3. Gaebler J. P. et al. Observation of pseudogap behaviour in a strongly interacting Fermi gas. Nature Physics, doi.org/10.1038/nphys1709
Journal information: Science , Nature Physics , Nature
© 2021 Science X Network