March 9, 2021 feature
Evidence of superfluidity in a dipolar supersolid
Superfluidity in liquids and gases can manifest as a reduced moment of inertia (the rotational analog of mass) under slow rotations. Non-classical rotational effects can also be considered in the elusive supersolid phases of matter where superfluidity can coexist with a lattice structure. In a new report now published in Science, L. Tanzi and a research team at the National Institute of Optics and the Department of Astronomy at the University of Florence in Italy, showed how a recently discovered supersolid phase in dipolar quantum gases featured a reduced moment of inertia. The team studied a peculiar rotational oscillation mode in a harmonic potential to deduce a supersolid fraction and provide direct evidence of the supersolid nature of the dipolar construct.
Superfluids and supersolidity
Superfluids exhibit their most spectacular properties during rotation, where the superfluid state is described by a macroscopic wavefunction. Physicists had already verified non-classical rotational effects for most known superfluids including nuclear matter, gaseous Bose-Einstein condensates and degenerate Fermi gases. The outcome is related to the Meissner effect noted in superconductors. In the 1960s, researchers discovered another type of bosonic phase of matter known as a supersolid, described by a macroscopic wavefunction. In a supersolid, superfluidity can coexist with a crystal-type architecture. Physicist suggested the rotating supersolid would show a moment of inertia intermediate to a superfluid and a classical system. This phenomenon is known as the non-classical rotational inertia (NCRI). These observations on supersolidity were primarily made using solid helium, where researchers employed torsion oscillators (rotational systems) to detect NCRI. In this work, Tanzi et al. investigated a different supersolid candidate – a gaseous Bose-Einstein condensate (BEC) of strongly dipolar atoms.
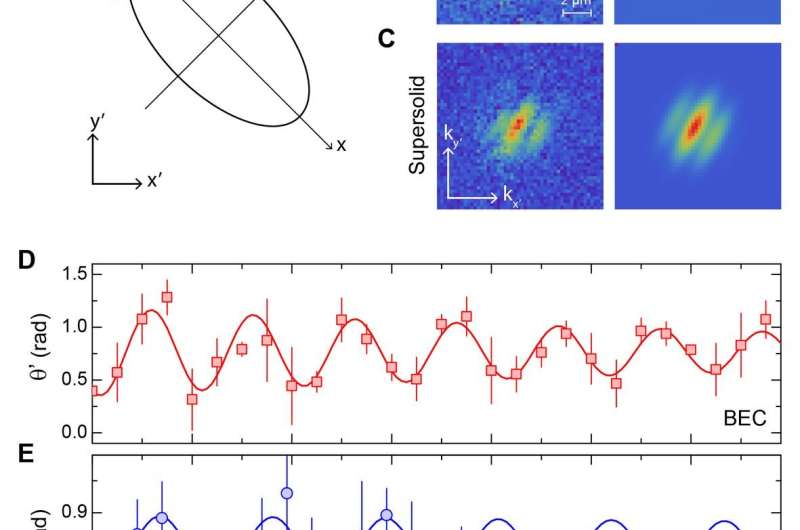
The BECs are formed at a fraction above absolute zero and only in atoms that act like bosons, one of two types of fundamental particles. When bosons are cooled to low-enough temperatures, a substantial fraction spontaneously enter a single quantum state in a phenomenon known as Bose–Einstein condensation (BEC), and the most famous experiments are those involving atomic gases. The recently discovered quantum system showed a density-modulated regime co-existing with the phase coherence, as required for supersolidity. Researchers had tested the superfluid nature using non-rotational excitation modes relative to hydrodynamic equations for superfluids. In keeping with preceding helium experiments, Tanzi et al. only focused on characterizing the NCRI (non-classical rotational inertia) of systems, in order to provide direct evidence of superfluidity under rotation.
The experiments
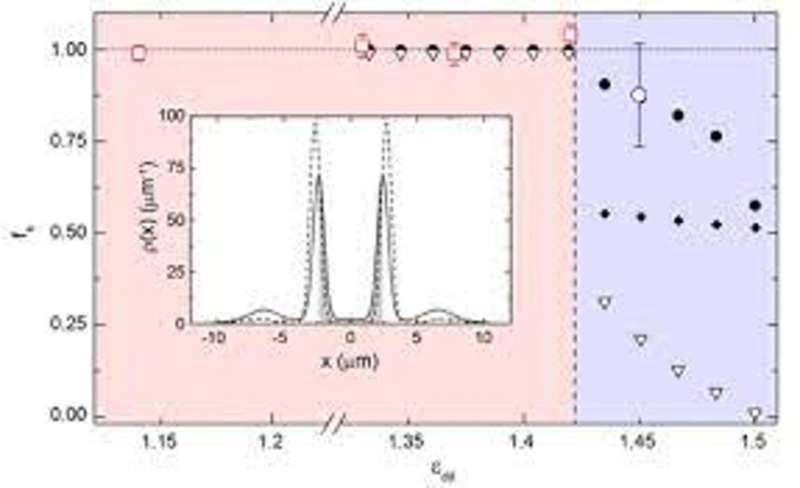
In quantum physics, It is still impractical to achieve dipolar solids large enough to realize a cylindrical geometry. As a result, the researchers selected a specific rotation technique to fit the asymmetric, small system in the lab. They then excited the so-called scissor-mode of the system; a small-angle rotational oscillation of the harmonic potential that naturally holds the system. The technique was previously employed to demonstrate superfluidity in ordinary Bose-Einstein condensates (BEC). Tanzi et al. investigated the changing scissor mode frequency across the transition from BEC to the supersolid form to directly compare the supersolid with a fully superfluid system. During the experiments, the team used a BEC of strongly magnetic Dysprosium (Dy) atoms in an anisotropic harmonic trap with frequencies with the dipoles oriented in the Z-direction via a magnetic field. The temperature of the system was sufficiently low and the scientists induced the transition from BEC to the supersolid by tuning via a magnetic Feshbach resonance and van der Waals interaction energies. The scientists expected the lattice to be composed of a cluster supersolid to bring the system into a droplet crystal regime without coherence between the droplets.
The scissor mode
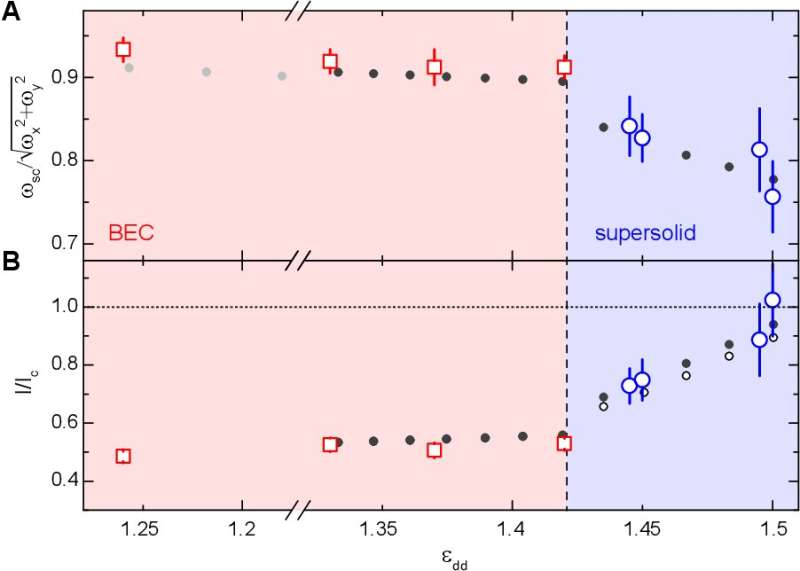
The team next excited the scissor mode and calculated the oscillation frequency to be directly related to the moment of inertia of the superfluid. They then connected the moment of inertia to a superfluid fraction specifically defined for the system. Tanzi et al. noted the analogy of the scissor mode to the helium torsion oscillators since both systems detected NCRI (non-classical rotational inertia) via the oscillation frequency. The experimental results summarized the scissors measurements in the BEC and supersolid regimes. The team imaged the 2-D density distributions after a free expansion of the system to represent effective momentum distributions. The BEC and supersolid regimes showed single-frequency oscillations as expected for weakly-interacting superfluids. To avoid disturbances caused by other collective modes in the system, Tanzi et al. employed two different excitation techniques for the BEC and the supersolid regimes. They then obtained a summary of the results for the scissor frequency and the related moment of inertia and then compared the outcomes with theoretical predictions. The team noted a clear reduction of the frequency when the system entered the supersolid regime in agreement with the theory. The outcomes provided further evidence of NCRI for the dipolar solid. The team explained the mechanisms shown in this work using original predictions made for Bose-condensation in condensed matter systems.
Outlook
In this way, L. Tanzi and colleagues established the superfluid nature of the dipolar supersolid by characterizing its non-classical rotational inertia. The supersolid was different from standard superfluids due to the reduced superfluid fraction. The technique detailed in this work will allow further investigations of the phenomena in future studies. The team propose achieving larger systems as an additional method to study the behavior of supersolids in annular geometry or in a 2-D configuration, while also studying the dynamics of quantized vortices in the supersolid phase.
More information:
1. Tanzi L. et al. Evidence of superfluidity in a dipolar supersolid from nonclassical rotational inertia, Science, DOI: 10.1126/science.aba4309
2. Lagoudakis K. G. et al. Quantized vortices in an exciton–polariton condensate, Nature Physics, doi.org/10.1038/nphys1051
3. Zwierlein M. W. et al. Vortices and superfluidity in a strongly interacting Fermi gas, Nature, 10.1038/nature03858
Journal information: Science
© 2021 Science X Network