New computing algorithms expand the boundaries of a quantum future
Quantum computing promises to harness the strange properties of quantum mechanics in machines that will outperform even the most powerful supercomputers of today. But the extent of their application, it turns out, isn't entirely clear.
To fully realize the potential of quantum computing, scientists must start with the basics: developing step-by-step procedures, or algorithms, for quantum computers to perform simple tasks, like the factoring of a number. These simple algorithms can then be used as building blocks for more complicated calculations.
Prasanth Shyamsundar, a postdoctoral research associate at the Department of Energy's Fermilab Quantum Institute, has done just that. In a preprint paper released in February, he announced two new algorithms that build upon existing work in the field to further diversify the types of problems quantum computers can solve.
"There are specific tasks that can be done faster using quantum computers, and I'm interested in understanding what those are," Shyamsundar said. "These new algorithms perform generic tasks, and I am hoping they will inspire people to design even more algorithms around them."
Shyamsundar's quantum algorithms, in particular, are useful when searching for a specific entry in an unsorted collection of data. Consider a toy example: Suppose we have a stack of 100 vinyl records, and we task a computer with finding the one jazz album in the stack.
Classically, a computer would need to examine each individual record and make a yes-or-no decision about whether it is the album we are searching for, based on a given set of search criteria.
"You have a query, and the computer gives you an output," Shyamsundar said. "In this case, the query is: Does this record satisfy my set of criteria? And the output is yes or no."
Finding the record in question could take only a few queries if it is near the top of the stack, or closer to 100 queries if the record is near the bottom. On average, a classical computer would locate the correct record with 50 queries, or half the total number in the stack.
A quantum computer, on the other hand, would locate the jazz album much faster. This is because it has the ability to analyze all of the records at once, using a quantum effect called superposition.
With this property, the number of queries needed to locate the jazz album is only about 10, the square root of the number of records in the stack. This phenomenon is known as quantum speedup and is a result of the unique way quantum computers store information.
The quantum advantage
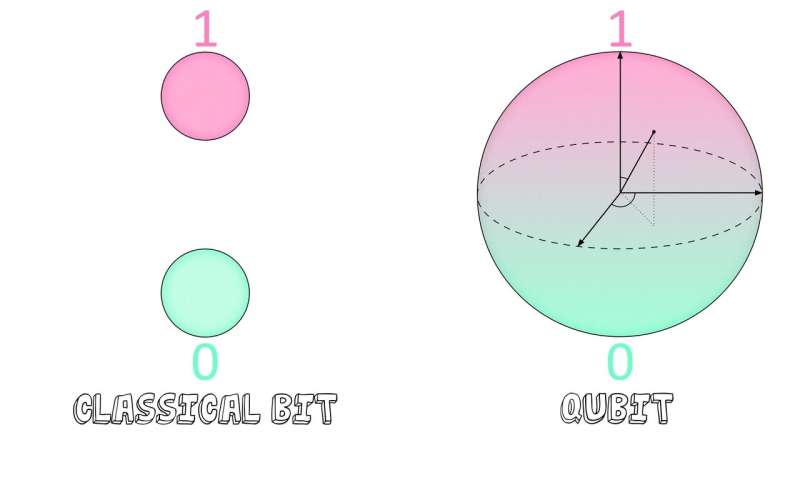
Classical computers use units of storage called bits to save and analyze data. A bit can be assigned one of two values: 0 or 1.
The quantum version of this is called a qubit. Qubits can be either 0 or 1 as well, but unlike their classical counterparts, they can also be a combination of both values at the same time. This is known as superposition, and allows quantum computers to assess multiple records, or states, simultaneously.
"If a single qubit can be in a superposition of 0 and 1, that means two qubits can be in a superposition of four possible states," Shyamsundar said. The number of accessible states grows exponentially with the number of qubits used.
Seems powerful, right? It's a huge advantage when approaching problems that require extensive computing power. The downside, however, is that superpositions are probabilistic in nature—meaning they won't yield definite outputs about the individual states themselves.
Think of it like a coin flip. When in the air, the state of the coin is indeterminate; it has a 50% probability of landing either heads or tails. Only when the coin reaches the ground does it settle into a value that can be determined precisely.
Quantum superpositions work in a similar way. They're a combination of individual states, each with their own probability of showing up when measured.
But the process of measuring won't necessarily collapse the superposition into the value we are looking for. That depends on the probability associated with the correct state.
"If we create a superposition of records and measure it, we're not necessarily going to get the right answer," Shyamsundar said. "It's just going to give us one of the records."
To fully capitalize on the speedup quantum computers provide, then, scientists must somehow be able to extract the correct record they are looking for. If they cannot, the advantage over classical computers is lost.
Amplifying the probabilities of correct states
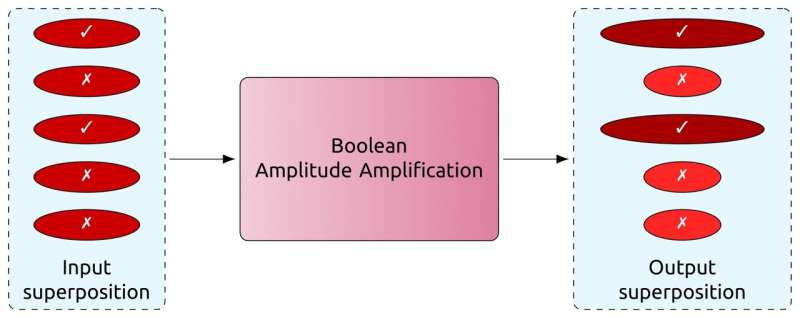
Luckily, scientists developed an algorithm nearly 25 years ago that will perform a series of operations on a superposition to amplify the probabilities of certain individual states and suppress others, depending on a given set of search criteria. That means when it comes time to measure, the superposition will most likely collapse into the state they are searching for.
But the limitation of this algorithm is that it can be applied only to Boolean situations, or ones that can be queried with a yes or no output, like searching for a jazz album in a stack of several records.
Scenarios with non-Boolean outputs present a challenge. Music genres aren't precisely defined, so a better approach to the jazz record problem might be to ask the computer to rate the albums by how "jazzy" they are. This could look like assigning each record a score on a scale from 1 to 10.
Previously, scientists would have to convert non-Boolean problems such as this into ones with Boolean outputs.
"You'd set a threshold and say any state below this threshold is bad, and any state above this threshold is good," Shyamsundar said. In our jazz record example, that would be the equivalent of saying anything rated between 1 and 5 isn't jazz, while anything between 5 and 10 is.
But Shyamsundar has extended this computation such that a Boolean conversion is no longer necessary. He calls this new technique the non-Boolean quantum amplitude amplification algorithm.
"If a problem requires a yes-or-no answer, the new algorithm is identical to the previous one," Shyamsundar said. "But this now becomes open to more tasks; there are a lot of problems that can be solved more naturally in terms of a score rather than a yes-or-no output."
A second algorithm introduced in the paper, dubbed the quantum mean estimation algorithm, allows scientists to estimate the average rating of all the records. In other words, it can assess how "jazzy" the stack is as a whole.
Both algorithms do away with having to reduce scenarios into computations with only two types of output, and instead allow for a range of outputs to more accurately characterize information with a quantum speedup over classical computing methods.
Procedures like these may seem primitive and abstract, but they build an essential foundation for more complex and useful tasks in the quantum future. Within physics, the newly introduced algorithms may eventually allow scientists to reach target sensitivities faster in certain experiments. Shyamsundar is also planning to leverage these algorithms for use in quantum machine learning.
And outside the realm of science? The possibilities are yet to be discovered.
"We're still in the early days of quantum computing," Shyamsundar said, noting that curiosity often drives innovation. "These algorithms are going to have an impact on how we use quantum computers in the future."
More information: Non-Boolean Quantum Amplitude Amplification and Quantum Mean Estimation. arXiv:2102.04975v1 [quant-ph] arxiv.org/abs/2102.04975
Provided by Fermi National Accelerator Laboratory