Implementing a quantum approximate optimization algorithm on a 53-qubit NISQ device

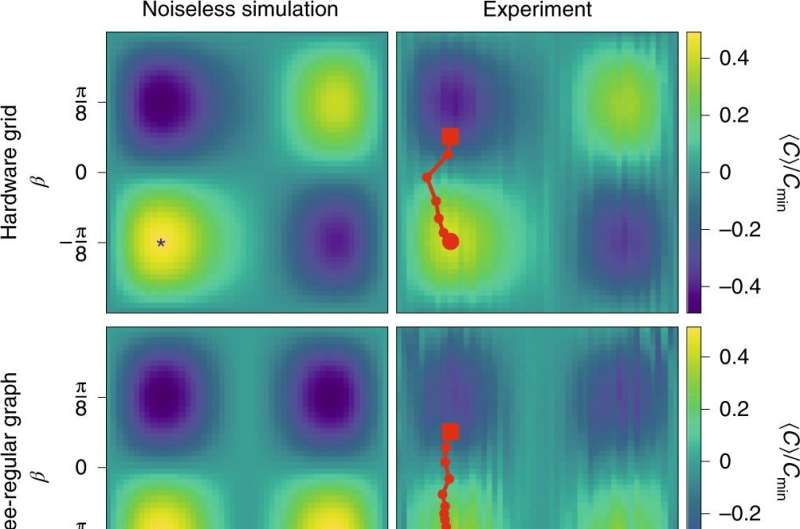
A large team of researchers working with Google Inc. and affiliated with a host of institutions in the U.S., one in Germany and one in the Netherlands has implemented a quantum approximate optimization algorithm (QAOA) on a 53-qubit noisy intermediate-scale quantum (NISQ) device. In their paper published in the journal Nature Physics,, the group describes their method of studying the performance of their QAOA on Google's Sycamore superconducting 53-qubit quantum processor and what they learned from it. Boaz Barak with Harvard University has published a News & Views piece on the work done by the team in the same journal issue.

Over the past several decades, engineers have made great strides in improving the speed of computers, even as they approach the ultimate limits of traditional silicon photolithography. So scientists have been working toward developing quantum computers, which theory has suggested could tackle applications that are still too difficult for computers to run. Unfortunately, despite some progress, quantum computers are still not truly useful. Those that have been built are described as NISQ devices, because they all suffer from the same problem—noise resulting in errors. They are also considered to be stepping-stones to the kinds of devices that theory suggests are possible—hence the intermediate label. As scientists continue to develop quantum computing technology, they are looking at what might be possible once such devices are built. To that end, they have been developing QAOAs—algorithms meant to bridge the computing gap between quantum computers and classical computers.

The reason QAOAs are needed is because engineers do not have any way to simulate NISQ devices on conventional computers, which makes it difficult to learn how to use a true quantum computer for real-world applications—the approximation algorithms help researchers get a better picture of what computing might be like when true quantum computers are finally up and running.

In this new effort, the researchers created a QAOA and ran it on Google's state of the art NISQ computing platform. As Barak notes, their QAOA worked as a combination of smaller algorithms that have been created to run simulations on a quantum computer, such as simulated annealing. Such algorithms begin by presenting a random answer and then seek to improve upon it using quantum operators. Using the algorithm, researchers learned more about ways to reduce noise or mitigate its effects. They also learned more about the use of hyperparameters and possible ways to map key problems onto a quantum architecture.

© 2021 Science X Network