Solving 'barren plateaus' is the key to quantum machine learning
Many machine learning algorithms on quantum computers suffer from the dreaded "barren plateau" of unsolvability, where they run into dead ends on optimization problems. This challenge had been relatively unstudied—until now. Rigorous theoretical work has established theorems that guarantee whether a given machine learning algorithm will work as it scales up on larger computers.
"The work solves a key problem of useability for quantum machine learning. We rigorously proved the conditions under which certain architectures of variational quantum algorithms will or will not have barren plateaus as they are scaled up," said Marco Cerezo, lead author on the paper published in Nature Communications today by a Los Alamos National Laboratory team. Cerezo is a post doc researching quantum information theory at Los Alamos. "With our theorems, you can guarantee that the architecture will be scalable to quantum computers with a large number of qubits."
"Usually the approach has been to run an optimization and see if it works, and that was leading to fatigue among researchers in the field," said Patrick Coles, a coauthor of the study. Establishing mathematical theorems and deriving first principles takes the guesswork out of developing algorithms.
The Los Alamos team used the common hybrid approach for variational quantum algorithms, training and optimizing the parameters on a classical computer and evaluating the algorithm's cost function, or the measure of the algorithm's success, on a quantum computer.
Machine learning algorithms translate an optimization task—say, finding the shortest route for a traveling salesperson through several cities—into a cost function, said coauthor Lukasz Cincio. That's a mathematical description of a function that will be minimized. The function reaches its minimum value only if you solve the problem.
Most quantum variational algorithms initiate their search randomly and evaluate the cost function globally across every qubit, which often leads to a barren plateau.
"We were able to prove that, if you choose a cost function that looks locally at each individual qubit, then we guarantee that the scaling won't result in an impossibly steep curve of time versus system size, and therefore can be trained," Coles said.
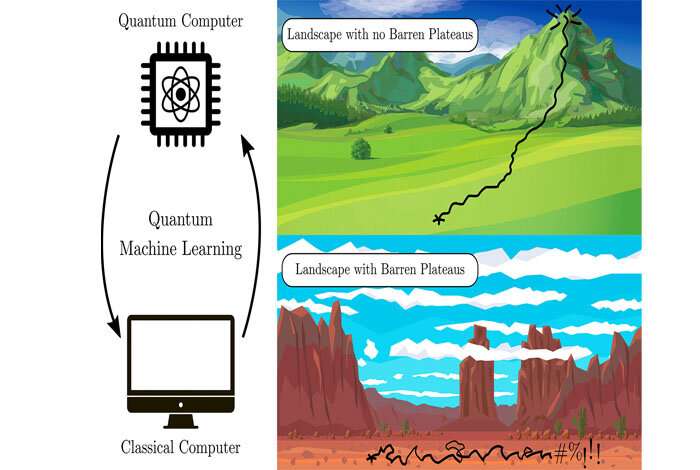
A quantum variational algorithm sets up a problem-solving landscape where the peaks represent the high energy points of the system, or problem, and the valleys are the low energy values. The answer lies in the deepest valley. That's the ground state, represented by the minimized cost function. To find the solution, the algorithm trains itself about the landscape, thereby navigating to the low spot.
"People have been proposing quantum neural networks and benchmarking them by doing small-scale simulations of 10s (or fewer) few qubits," Cerezo said. "The trouble is, you won't see the barren plateau with a small number of qubits, but when you try to scale up to more qubits, it appears. Then the algorithm has to be reworked for a larger quantum computer."
A barren plateau is a trainability problem that occurs in machine learning optimization algorithms when the problem-solving space turns flat as the algorithm is run. In that situation, the algorithm can't find the downward slope in what appears to be a featureless landscape and there's no clear path to the energy minimum. Lacking landscape features, the machine learning can't train itself to find the solution.
"If you have a barren plateau, all hope of quantum speedup or quantum advantage is lost," Cerezo said.
The Los Alamos team's breakthrough takes an important step toward quantum advantage, when a quantum computer performs a task that would take infinitely long on a classical computer. Achieving quantum advantage hinges in the short term on scaling up variational quantum algorithms. These algorithms have the potential so solve practical problems when quantum computers of 100 qubits or more become available—hopefully soon. Quantum computers currently max out at 65 qubits. A qubit is the basic unit of information in a quantum computer, as bits are in a classical digital computer.
"The hottest topic in noisy intermediate-scale quantum computers is variational quantum algorithms, or quantum machine learning and quantum neural networks," Coles said. "They have been proposed for applications from solving the structure of a molecule in chemistry to simulating the dynamics of atoms and molecules and factoring numbers."
More information: M. Cerezo et al, Cost function dependent barren plateaus in shallow parametrized quantum circuits, Nature Communications (2021). DOI: 10.1038/s41467-021-21728-w
Journal information: Nature Communications
Provided by Los Alamos National Laboratory