A new mathematical front to understand species coexistence
How biodiversity is generated and maintained are central questions in science, which are becoming increasingly important for our quality of life. How do similar species coexist in a system? Which ones will dominate or be excluded? Will the system succumb to invasion by outsiders? Can we predict these interactive dynamics in systems with many different species? Simulations and statistical approaches are typically adopted to answer these questions, but the limited predictions they offer prompted Erida Gjini, principal investigator at Instituto Gulbenkian de Ciência, in collaboration with Sten Madec, from the University of Tours, in France, to explore a deeper mathematical route and uncover the general rules that describe such systems.
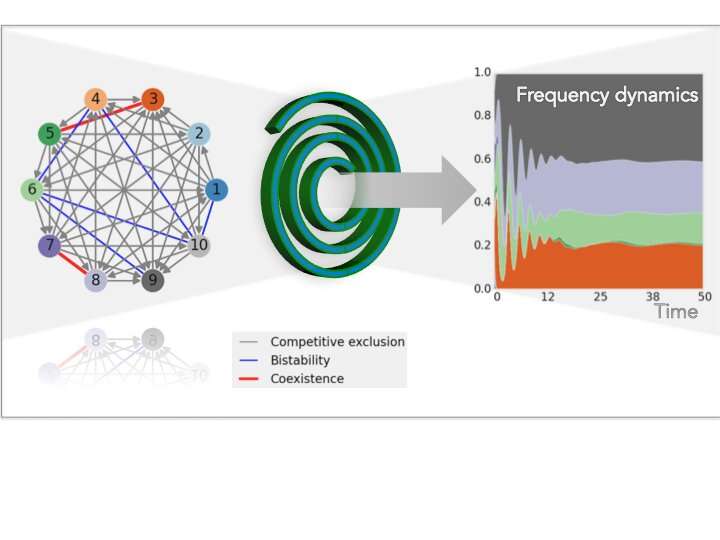
The two researchers used the system of microbial transmission between hosts as the basis of their theoretical study. In this type of system, each species colonizing the host can alter the local environment and make it better or worse for co-colonization by another species. If made better, it is described as pairwise facilitation; if made worse, it reflects pairwise competition. This study proposes a framework that addresses what is the final outcome in a network of many pairwise interactions and how its members 'engineer' together their coexistence.
"In the beginning we did not know how the pairwise competition or facilitation between all interacting members translated into the global dynamics of the system. We were dealing with many equations and their number rose quadratically with the number of species we considered in our model. For example, for 10 species we would have more than 100 equations to deal with," stated Erida Gjini. The mathematical technique of time-scale separation offered an advantage here, since it allows the separation of the variables that change faster from the ones that change slower.
"Thanks to this method we uncovered a simple equation that belongs to the family of the replicator equations (widely used in evolutionary game theory), which governs frequency dynamics between species in our model. This type of equations captures the essence of the competition between multiple strategies in a multi-player game and how their success changes over time. Surprisingly, we find it here, emerging from the matrix of 'social' interactions," explains Erida Gjini. With these results, it becomes clear that global dynamics of the system can be predicted entirely from the type and quality of pairwise interactions.
"We believe this will change the way people study multi-type communities, beyond epidemiology, which was the initial motivation for this work. On a more fundamental level, the mathematical language of this work ultimately conveys that we do not live alone, but are embedded in a network of inter-dependencies with others, where individual success depends on proximal connections, but also on the global emerging context," highlight the authors. This framework brings analytical and computational advantages for studying and interpreting high-dimensional interacting systems, especially in what regards their stability and evolution, establishing co-colonization as an important route to coexistence and biodiversity.
More information: Sten Madec et al, Predicting N-Strain Coexistence from Co-colonization Interactions: Epidemiology Meets Ecology and the Replicator Equation, Bulletin of Mathematical Biology (2020). DOI: 10.1007/s11538-020-00816-w
Provided by Instituto Gulbenkian de Ciencia