September 15, 2020 feature
Predicting delayed instabilities in viscoelastic solids
It is presently challenging to determine the stability of viscoelastic structures since seemingly stable conformations may gradually creep (plastic deformation of a material under stress as a function of time) until their stability is lost. Although a discernable creeping effect does not necessarily lend to instability of viscoelastic solids, researchers are currently limited with numerical simulations to predict the future stability relative to theoretical predictive tools. In a new report on Science Advances, Erez Y. Urbach and Efi Efrati in physics and complex systems at the Weizmann Institute of Science, Israel, described viscoelastic solids through an evolving instantaneous reference metric to measure elastic strains. The transparent and intuitive methods derived in this work for incompressible viscoelastic solids reduced the question of future stability to static calculations alone. The team showed the predictive power of the approach by understanding the subtle mechanisms of delayed instability in thin elastomeric shells in order to demonstrate quantitative agreement with experiments.
Creeping motion in nature
A relatively slow creeping motion underlies the snapping Venus fly-trap – one of the fastest motions in the plant kingdom. Similar creep is observed prior to thin elastomeric shells snapping, known as jumping poppers that last a fraction of a second. While the slow creeping motion of shells appear to be elastically stable, lasting orders of magnitude longer, those on a much larger scale can be noted on Earth's crust before an earthquake aftershock. Researchers are still learning the exact role of viscoelasticity in aftershocks due to the absence of a predictive theoretical framework to detect the future stability of such systems. In each of the outlined examples, the slow viscoelastic flow in the material can lead the system to instabilities, causing an abrupt release of internally stored elastic energy. Although scientists can determine the variables governing viscoelastic behavior, the mechanisms of delayed instabilities in viscoelastic fluids remain poorly understood. In this work, Urbach and Efrati quantitatively addressed the feature of viscoelastic instability by using a metric description.
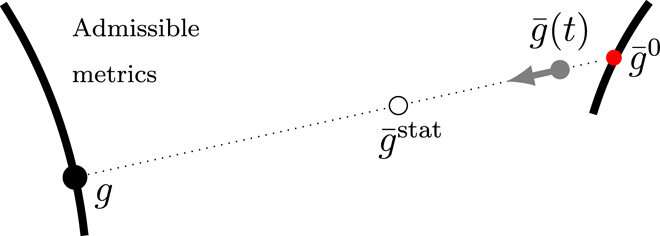
The team described the materials' behavior as a fast elastic response relative to temporally evolving test lengths that can change due to slow viscoelastic flow. They interpreted the microscopic response in the material and predicted the future stability of unconstrained viscoelastic structures. Urbach et al. explained all relations of linear viscoelastic materials through intricate calculations of strain rate with a stress relaxation function, then derived mathematical relationships for one-dimensional systems in this work; some of which depended on material properties such as the Young's modulus and the Poisson's ratio. Instantaneous incremental deformations caused increased linear stress for a purely elastic response in the material. Since viscoelastic materials tend to be dissipative (thermodynamically open), the definition of an elastic free energy can be incomplete. The scientists therefore eliminated inertia from the system and approximated the motion of the material to a quasi-state evolving between elastic equilibrium states. As a result, a given instantaneous reference metric could yield multiple elastically stable configurations.
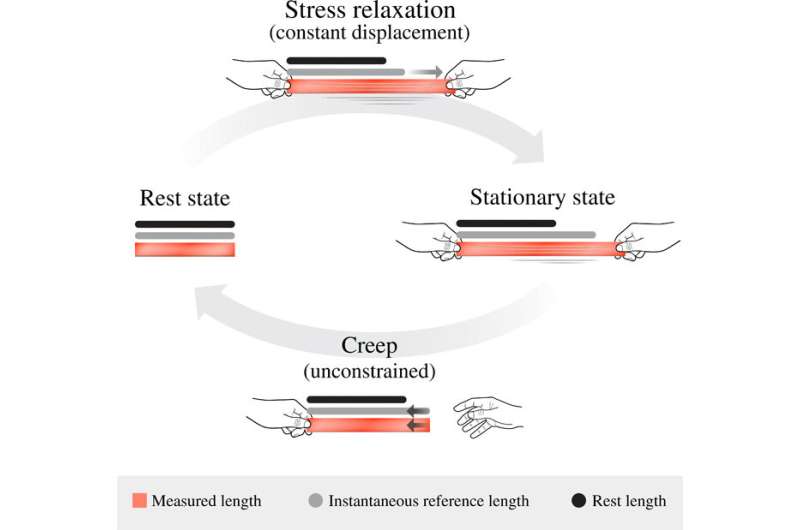
Viscoelastic instabilities through the metric description
The time-dependent instantaneous reference metric of the material could in this way evolve to acquire new stable configurations, merge existing stable points, or cause stable elastic configurations to lose stability. In the latter scenario, the slow viscoelastic evolution will be followed by a rapid snap—highlighting the main difficulty of predicting the stability of viscoelastic structures. This feature is known as temporary bistability, pseudo bistability or creep buckling. Two distinct processes must take place for incompressible linearly viscoelastic solids to creep into instability. First, an elastically stable state will acquire stability through viscoelastic relaxation under some external load for an amount of time. Then as the external load is removed, the body will assume the newly acquired stable state, alongside viscoelastic creep for the resulting instability. However, an acquired stable state is transient (temporary). In this way, Urbach et al. used the metric description of viscoelasticity to provide a picture of the mechanism governing the stability of viscoelastic structures.
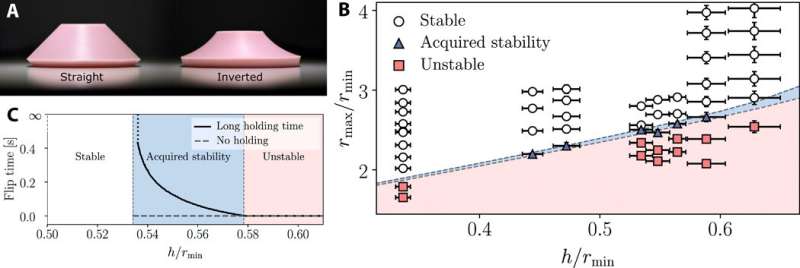
Experimental results
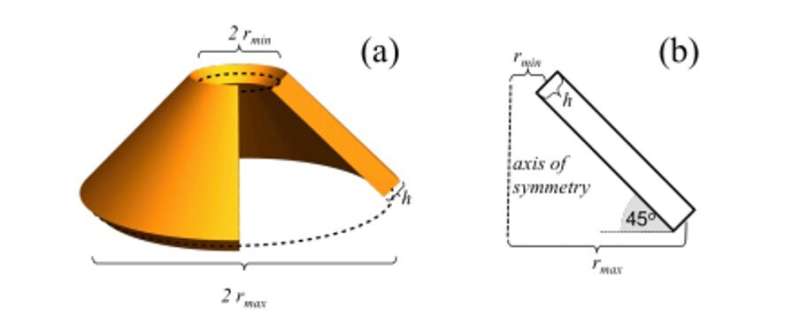
The calculations conducted in this work revealed many qualitative characteristics of viscoelastic instabilities. The scientists then tested the quantitative predictions of the theory by experimentally examining the response of silicone rubber conical poppers. For this, they cast silicon rubber poppers as truncated conical shells to gain simpler control on the thickness of the material. As the thickness increased, the bistability decreased, then at a timepoint the popper immediately snapped back. The scientists produced 50 different conical poppers of different geometries and tested their phases to experimentally determine the phase boundaries of viscoelastic properties.
The work presented here was similar to previous studies on elastoplasticity. The metric theory can be implemented to isotropic incompressible viscoelastic solids to provide basic rules for viscoelastic instabilities. In order for a given structure to creep into instability, the creeping should have preceded within a timeframe in which the structures were held under an external load. The theory was specifically powerful on application to describe the experimentally delayed instability in thin elastomeric shells. These results will be able to shed light on the role of viscoelasticity in triggering delayed earthquake aftershocks. In this way, the metric description proposed here will provide a theoretical framework to understand delayed viscoelastic instabilities.
More information: Erez Y. Urbach et al. Predicting delayed instabilities in viscoelastic solids, Science Advances (2020). DOI: 10.1126/sciadv.abb2948
Yoël Forterre et al. How the Venus flytrap snaps, Nature (2005). DOI: 10.1038/nature03185
Michael Gomez et al. Critical slowing down in purely elastic 'snap-through' instabilities, Nature Physics (2016). DOI: 10.1038/nphys3915
Journal information: Science Advances , Nature , Nature Physics
© 2020 Science X Network