April 29, 2020 feature
Quantum autoencoders to denoise quantum measurements
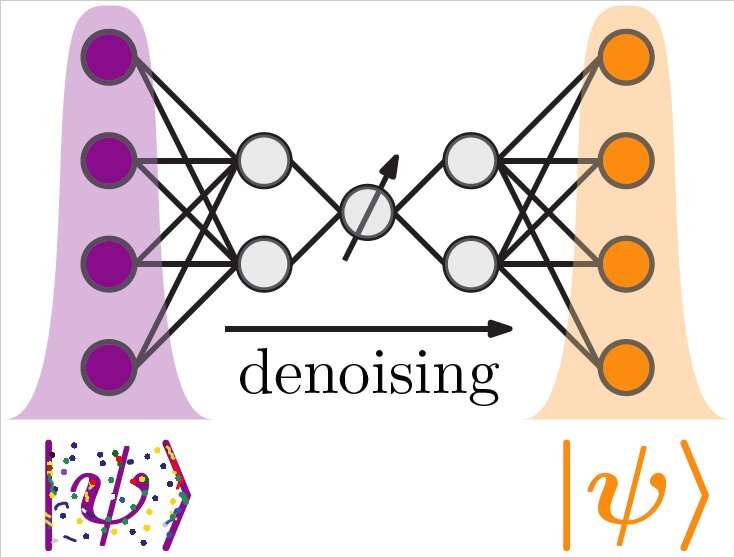
Many research groups worldwide are currently trying to develop instruments to collect high-precision measurements, such as atomic clocks or gravimeters. Some of these researchers have tried to achieve this using entangled quantum states, which have a higher sensitivity to quantities than classical or non-entangled states.
Due to this high sensitivity, however, quantum entangled states are also more susceptible to picking up noise (i.e., unrelated signals) while collecting measurements. This can hinder the development of accurate and reliable quantum-enhanced metrological devices.
To overcome this limitation, two researchers at Leibniz Universität Hannover in Germany have recently developed quantum machine-learning algorithms that can be used to denoise quantum data. These algorithms, presented in a paper published in Physical Review Letters, could help to produce more reliable data using quantum clocks or other measurement tools based on entangled quantum states.
Dmytro Bondarenko, one of the researchers involved in the study, had already been working on a new algorithm based on quantum machine learning under the supervision of Professor Tobias Osborne at Leibniz Universität, Hannover. In this new study, Bondarenko and his colleague Polina Feldmann set out to investigate the feasibility of using this algorithm to denoise data collected by quantum-enhanced instruments.
"Quantum machine learning is a very promising topic, as it can combine the versatility of machine learning with the power of quantum algorithms," Bondarenko and Feldmann told Phys.org via email. "Machine learning is a ubiquitous method for data analysis."
Just like traditional machine-learning algorithms, quantum machine-learning algorithms depend on a series of variational parameters that need to be optimized before an algorithm can be used to analyze data. To learn the correct parameters, the algorithm needs first to be trained on data related to the task it is designed to complete (e.g., pattern recognition, image classification, etc.).
"When we say quantum machine learning, we mean that the input and the output of the algorithm are quantum states, for example, of some number of qubits (quantum bits), which can be realized, for instance, using superconductors," Bondarenko and Feldmann said. "The algorithm that maps the input state to the output state is meant to be implemented on a quantum computer. The variational parameters, which have to be optimized, are classical parameters of the transformations that are performed on the quantum computer."
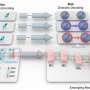
The two researchers wanted to test whether the quantum machine leaning algorithm previously developed by Bondarenko, Osborne and their other colleagues could be used to clean up data collected using quantum-enhanced metrology tools. This ultimately led to the development of the quantum autoencoders introduced in their recent paper.
"Assume that you have a quantum experiment that gives you a number of noisy quantum states," Bondarenko and Feldmann explained. "Assume furthermore that you have a quantum computer which can process these states. Our autoencoder is an algorithm which tells the quantum computer how to transform the noisy quantum states from the experiment to denoise them."
As an initial step in their research, Bondarenko and Feldmann optimized their algorithms, training them to effectively denoise quantum data. As denoised reference states are hard to obtain or unavailable experimentally, the researchers used a trick that is often used when optimizing classical autoencoders, which are a type of unsupervised machine-learning algorithms.
"The trick is that the algorithm is written in such a way that it has to reduce the information on the way from the input to its output state," Bondarenko and Feldmann said. "Now, the figure of merit is defined as the similarity of the state processed by the autoencoder and another noisy state from your experiment. To make these states as similar as possible, the autoencoder has to keep the information which is equal for both states (their common noiseless origin), while discarding the noise, which, in every state coming from your experiment, is different."
The researchers have carried out numerous simulations in which they produced noisy entangled quantum states. First, they used these 'experimental' outputs to optimize the variational parameters of the autoencoder. Once this training phase was complete, they were able to evaluate their autoencoders' performance in denoising quantum measurements.
"The beauty of our approach is its generality," Bondarenko and Feldmann said. "You do not need to know beforehand what the output from your experiment looks like, nor do you have to characterize your noise sources. The denoising works even if your experimental output is not unique but depends on some experimental control parameter, which is crucial for metrological applications."
The goal of the numerical experiments was to denoise a number of highly entangled quantum states that are subject to spin-flip errors and random unitary noise. Their algorithms achieved remarkable results and could also be implemented on current quantum devices.
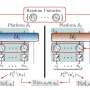
The algorithms require a quantum computer that can process the specific experimental output (i.e., quantum data). For instance, if a researcher is trying to use the autoencoders to denoise data based on trapped ions, but her quantum computer uses superconducting qubits, she will also need to use a technique that can map states from one physical platform to the other.
"Effectively training our autoencoders requires several trials, a considerable amount of experimental data, and the ability to measure the similarity between quantum states," Bondarenko and Feldmann said. "Nonetheless, our algorithm isn't too wasteful regarding these resources and our examples are small enough to easily fit, at least in terms of the number of qubits, into many existing quantum computers."
While quantum machine learning techniques and quantum computers have been found to perform well in a variety of tasks, researchers are still trying to identify the practical applications for which they could be of most use. The recent study carried out by Bondarenko and Feldmann offers a clear example of how quantum machine learning methods could ultimately be used in real-world scenarios.
"It was not at all obvious that our approach would work; and it does more than just work, at least in our small examples, it works extremely well," Bondarenko and Feldmann said.
In the future, the quantum autoencoders developed by these two researchers could be used to improve the reliability of measurements collected using quantum-enhanced tools, particularly those using many-body entangled states. In addition, they could serve as interfaces between different quantum architectures.
"Different quantum devices have different merits," Bondarenko and Feldmann said. "For example, it might be easier to use cold atoms to measure gravity, photons are great for communication and superconducting qubits are more useful for the quantum information processing. To convert information exchanged between these different platforms we need interfaces, which, by themselves, introduce errors. Our autoencoders can help to denoise this exchanged data."
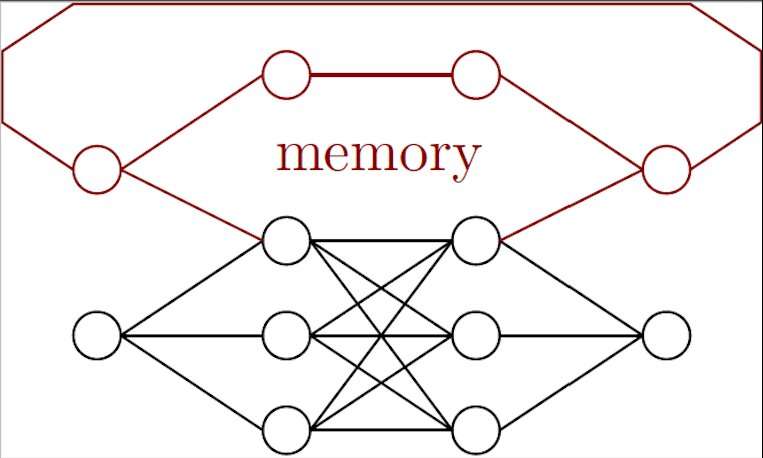
Bondarenko and Feldmann are now trying to develop a different type of quantum algorithm: a recurrent quantum neural network. This new algorithm's recurrent architecture should allow it to store information it processed in the past and have a 'memory," which would allow the researchers to correct for drifts.
"This can make the quantum experiments simpler because drifts will be filtered away by post processing," Bondarenko and Feldmann said. "Another application of recurrent neural networks is the denoising in the case of slowly changing noise. For example, if one sends entangled photons via air, noise can differ between a snowy cloudy day and a hot day. However, the weather cannot change instantaneously, so an algorithm with memory can outperform one without."
More information: Dmytro Bondarenko et al. Quantum Autoencoders to Denoise Quantum Data, Physical Review Letters (2020). DOI: 10.1103/PhysRevLett.124.130502 journals.aps.org/prl/abstract/ … ysRevLett.124.130502
Kerstin Beer et al. Training deep quantum neural networks, Nature Communications (2020). DOI: 10.1038/s41467-020-14454-2 www.nature.com/articles/s41467-020-14454-2
Journal information: Physical Review Letters , Nature Communications
© 2020 Science X Network