New mathematical model for amyloid formation
Amyloids are aggregates consisting of stacks of thousands of proteins bound tightly together. Their formation is involved in several widespread disorders, including Alzheimer's disease and Type II diabetes.
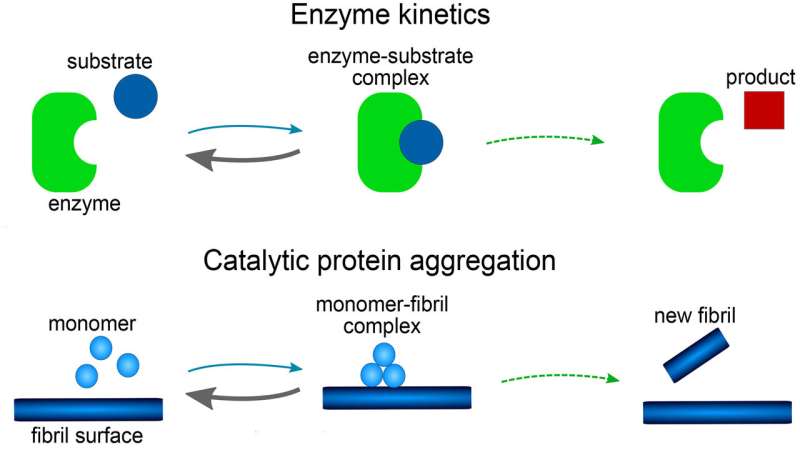
In this week's Journal of Chemical Physics scientists report on a mathematical model for the formation of amyloid fibrils. The model sheds light on how the aggregation process can occur in a catalytic manner, something that has not been previously well understood.
The investigators applied their model to the aggregation of a specific protein associated with Alzheimer's, Ab40. The results show the initiation of the aggregation process for Ab40?fibrils typically occurs at interfaces, such as near the surface of a liquid solution or the glass wall of a test tube. This has important implications for the interpretation of laboratory data used in the study of Alzheimer's and other diseases.
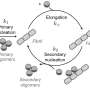
The model consists of a set of mathematical equations, known as rate equations, that describe how protein aggregate concentrations change over time. Each reaction step in the model is shown to be analogous to those in reactions involving enzymes. The role of the enzyme is played by either the tip or side of a growing fiber or, possibly, a surface of the reaction vessel.
The investigators found the mathematical form of their model was related to the famous Michaelis-Menten equations, first published in 1913 to describe the rates of enzyme reactions. It has a far simpler mathematical form than all previous models used for amyloid formation and has the additional advantage that the equations can be solved by hand, without the need for computer simulations.
"We expect the methodology developed in this paper will underpin future efforts to model new amyloid formation phenomena," co-author Alexander Dear said.
One of the key features of the mathematical solution found for Michaelis-Menten-type equations is a phenomenon known as saturation. When saturation occurs, the catalytic sites become fully occupied at high protein concentrations. In the case of the Ab40 studies, saturation also shows that the process initiating aggregation involves a surface, such as the wall of a test tube.
While the conclusions do not directly apply to the body itself, co-author Tuomas Knowles said, "This work will be central in facilitating the study of amyloid formation in the presence of other species found in body fluids."
Co-author Sara Linse said, "This work takes the analysis of experimental data to a new level that will be essential for deriving potent inhibitors of amyloid formation."
More information: The catalytic nature of protein aggregation, Journal of Chemical Physics (2020). DOI: 10.1063/1.5133635
Journal information: Journal of Chemical Physics
Provided by American Institute of Physics