The physical limit of quantum optics resolves a mystery of computational complexity
Linear optics comprises one of the best examples for demonstrating quantum physics. It works at room temperatures, and can be observed with relatively simple devices. Linear optics involves physical processes that conserve the total number of photons. In the ideal case, if there are 100 photons at the beginning, no matter how complicated the physical process is, there will be exactly 100 photons left in the end.
Photons are bosonic non-interacting particles. However, they can still interference with each other, exhibiting non-trivial quantum effects. A typical example is the Hong-Ou-Mandel experiment, where two identical photons are sent to an experimental device. After a simple linear transformation, the two photons appear as if they are stuck together and unwilling to separate. In addition to providing a foundational understanding of quantum mechanics, the study of linear optics has also led to many scientific applications.
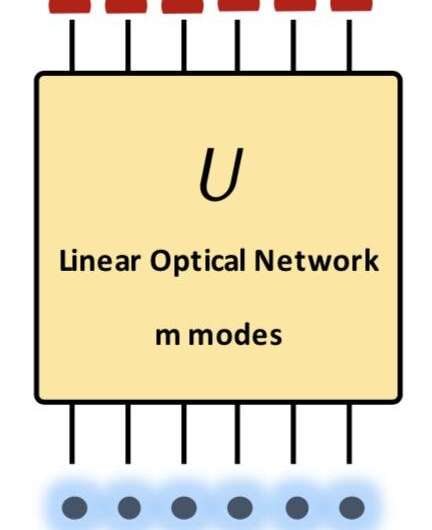
In recent years, the unique properties of linear optical systems have also inspired the development of computational complexity theory. In 2012, Professor Scott Aaronson at MIT (currently at the University of Texas at Austin) proposed a linear optical method for demonstrating the quantum (computational) supremacy, which is based on the concept of boson sampling. More specifically, Aaronson suggested that for a class of sampling problems based on linear optical systems, it would be impossible in practice to apply any classical computer to simulate. This idea immediately sparks a race for reaching the status of "quantum supremacy." Many quantum optical laboratories around the world have become interested in developing boson sampling systems to break records in terms of photon numbers. On the other hand, computer scientists are busy in applying supercomputers to raise the bar for achieving quantum supremacy.
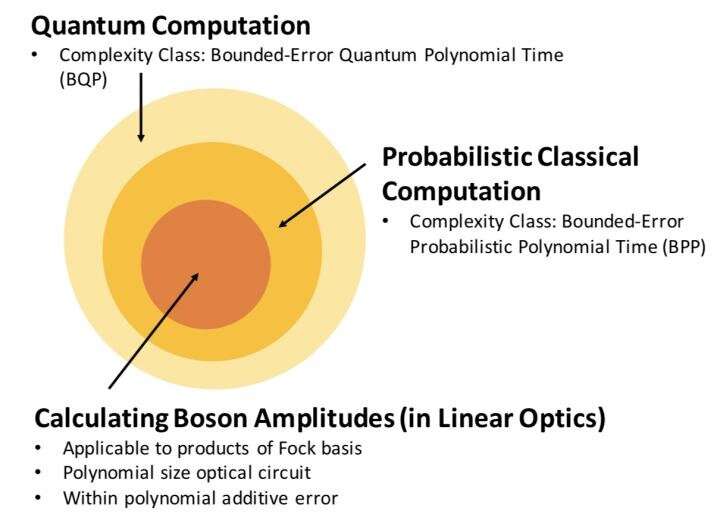
However, in terms of practical problems, applying the model of boson sampling is not a good approach. Therefore, Aaronson raised a question in 2012: Apart from sampling problems, can researchers exploit linear optics to achieve quantum supremacy in terms of decision problems with a YES/NO answer? Recently, Prof. Man-Hong Yung, associate professor of SUSTech and his colleagues published a paper titled "Universal bound on sampling bosons in linear optics and its computational implications" in National Science Review (NSR), offering a complete solution to the open problem posed by Aaronson.
Specifically, Yung's team uncovered a fundamental limit on the transition probabilities of linear optical systems, constraining the ability to transfer bosons using linear optical devices. Together with the tools of quantum optics, they developed a classical algorithm that can efficiently estimate the transition amplitude with a bounded error. Consequently, these results lead to a negative answer to Aaronson's open problem. In other words, for encoding hard decision problems,it is necessary to make use of more complicated quantum optics systems instead of just linear optics.
As an interdisciplinary domain between quantum physics and computer science, quantum information science remains to be a highly active research area. On one hand, the results of Yung's team contribute to the theoretical foundation of quantum optics; on the other hand, in addition to boson sampling, these results point to a novel perspective on computational complexity problems in terms of quantum optics. Undoubtedly, in the future, we should expect to see many more exciting results like these in this area.
More information: Man-Hong Yung et al, Universal Bound on Sampling Bosons in Linear Optics and Its Computational Implications, National Science Review (2019). DOI: 10.1093/nsr/nwz048
Provided by Science China Press