May 22, 2019 feature
Physicists propose a second level of quantization for quantum Shannon theory
Information theory, which was developed by Claude Shannon starting in the late 1940s, deals with questions such as how quickly information can be sent over a noisy communications channel. Both the information carriers (e.g., photons) and the channel (e.g., optical fiber cable) are assumed to be classical systems, with well-defined, perfectly distinguishable states.
In the past two decades, physicists have been developing a quantum version of information theory in which the internal state of each information carrier has quantum properties, such as superposition—the ability to occupy two or more classical states at once. But the transmission lines are generally still assumed to be classical, so that the path taken by messages in space is always well-defined.
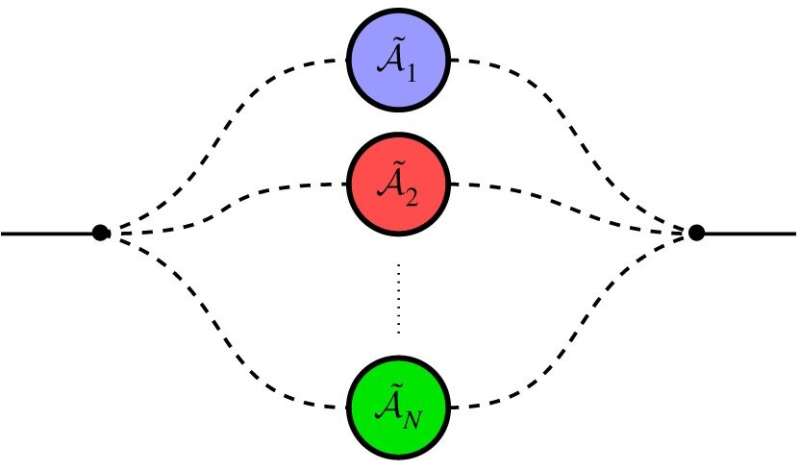
Now in a new paper, physicists Giulio Chiribella and Hlér Kristjánsson at the University of Oxford and the University of Hong Kong have proposed a second level of quantization, in which both the information carriers and the channels can be in quantum superposition. In this new paradigm of communication, the information carriers can travel through multiple channels simultaneously.
"This work provides the foundation for a new theory of communication where the propagation of information in space and time is treated quantum mechanically," Chiribella told Phys.org. "It opens up new avenues for quantum communication networks and for a future quantum internet, where data could be sent from a sender to a receiver through multiple quantum servers. Exploiting the interference of different communication paths, it will be possible to communicate more efficiently and more securely. At the fundamental level, the transmission of messages along multiple trajectories could give rise to fundamental tests of the quantum nature of spacetime."
This channel superposition phenomenon can be observed in the famous double-slit experiment, in which a single photon seems to pass through two slits at once. Even though just a single photon is used, the photon creates an interference pattern on the detector. The best explanation for the interference pattern is that the photon interfered with itself, like a wave, after simultaneously traveling through both slits along two different paths.
When an information carrier is allowed to travel through two communications channels simultaneously, it can offer advantages such as reduced noise (due to the interference of noise on different paths) and a higher channel capacity. These advantages have been demonstrated in recent experiments with photons.
In the new paper, the physicists had to confront some of the challenges involved in incorporating the superposition of channels into a quantum theory of information. One of the challenges is to describe the superposition of channels in a compositional way, so that the behavior of a channel can be predicted when it is used in combination with other channels. A second challenge is that the superposition of internal states of the information carriers must be clearly separated from the superposition of paths. Otherwise, the path itself becomes part of the message, and the system can be described using the conventional quantum framework.
By addressing these challenges, the physicists formulated a quantum communications model that can be used to compute the amount of information that can be reliably transmitted when using a given number of channels in a quantum superposition. Counterintuitively, the physicists showed that, for certain types of noise, the superposition of channels, along with the ability to switch a channel with itself, could be used to completely remove all noise. This opens up the possibility of obtaining perfect quantum communication in a noisy channel.
"Our work defined a communication model and provided a few proof-of-principle examples," Chiribella said. "However, this has only scratched the surface of what can be accomplished with the superposition of quantum communication channels. We are now exploring the power of correlations among them. If two trajectories visit the same region, the process experienced by the information carrier in the first trajectory can be correlated with the process experienced in the second trajectory. By taking advantage of these correlations in a clever way, it is possible to enhance the communication performance beyond what can be done with the superposition of independent channels. Getting ahold of these correlations will give us new insights into the peculiar ways in which quantum information propagates in space and time."
More information: Giulio Chiribella and Hlér Kristjánsson. "Quantum Shannon theory with superpositions of trajectories." Proceedings of the Royal Society A. DOI: 10.1098/rspa.2018.0903
Journal information: Proceedings of the Royal Society A
© 2019 Science X Network