Understanding insulators with conducting edges
Insulators that are conducting at their edges hold promise for interesting technological applications. However, until now their characteristics have not been fully understood. Physicists at Goethe University have now modelled what are known as topological insulators with the help of ultracold quantum gases. In the current issue of Physical Review Letters, they demonstrate how the edge states could be experimentally detected.
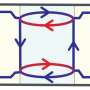
Imagine a disc made of an insulator with a conducting edge along which a current always flows in the same direction. "This makes it impossible for a quantum particle to be impeded, because the state of flowing in the other direction simply doesn't exist," explains Bernhard Irsigler, the first author of the study. In other words: in the edge state, the current flows without resistance. This could be used, for example, to increase the stability and energy efficiency of mobile devices. Research is also being done on how to use this to construct lasers that are more efficient.
In recent years, topological insulators have also been produced in ultracold quantum gases in order to better understand their behaviour. These gases result when a normal gas is cooled down to temperatures between a millionth and billionth of a degree above absolute zero. This makes ultracold quantum gases the coldest places in the universe. If an ultracold quantum gas is also produced in an optical lattice made of laser light, the gas atoms arrange themselves as regularly as in the crystal lattice of a solid. However, unlike a solid, many parameters can be varied, allowing artificial quantum states to be studied.
"We like to call it a quantum simulator because this kind of system reveals many things that take place in solids. Using ultracold quantum gases in optical lattices, we can understand the basic physics of topological insulators," explains co-author Jun-Hui Zheng.
A significant difference between a solid and a quantum gas, however, is that the cloud-shaped gases do not have defined edges. So how does a topological insulator in an ultracold gas decide where its edge states are? The researchers in Professor Walter Hofstetter's research group at the Institute for Theoretical Physics at Goethe University answer this question in their study. They modelled an artificial barrier between a topological isolator and a normal isolator. This represents the edge of the topological insulator along which the conducting edge state forms.
"We demonstrate that the edge state is characterized through quantum correlations that could be measured in an experiment using a quantum gas microscope. Harvard University, MIT and the Max-Planck-Institute for Quantum Optics in Munich all carry out these kinds of measurements," says Hofstetter. A quantum gas microscope is an instrument with which individual atoms can be detected in experiments. "For our work, it is critical that we explicitly take into account the interaction between the particles of the quantum gas. That makes the investigation more realistic, but also much more complicated. The complex calculations could not be carried out without a supercomputer. The close collaboration with leading European scientists within the context of the DFG Research Unit 'Artificial Gauge Fields and Interacting Topological Phases in Ultracold Atoms' is also of particular importance for us," Hofstetter adds.
More information: Bernhard Irsigler et al. Interacting Hofstadter Interface, Physical Review Letters (2019). DOI: 10.1103/PhysRevLett.122.010406
Journal information: Physical Review Letters
Provided by Goethe University Frankfurt am Main