Determining the shape of cells
Cells are constantly performing small tasks such as repairing wounds. They exert force by changing shape. But how do cells translate their shape into exerting a force in a specific direction? Experimental and theoretical physicists from Leiden University have now found a clue to answer this question. Cells' shapes turn out to be approximated by arcs of an ellipse. The research was published in Physical Review Letters on October 29th.
Suppose you trip on the sidewalk and get a small graze wound on your elbow. What do you do? Perhaps you should disinfect it, but for the rest: leave it alone. Before we get a chance to think about it, millions of fibroblast cells have already started the healing process. Among other things, they close the small gaps in the skin by pulling tissue together. Cells perform this job, like all of their other jobs, by changing their shape. It enables them to exert force and sense their surroundings. People actually do the same thing—they change their posture while fixing a tire or search for the alarm clock in the dark. But how do cells translate their shape into applying a force in a specific direction? A collaboration of experimental and theoretical physicists from Leiden University now reports an answer this question. The team, led by Luca Giomi and Thomas Schmidt, discovered that the shape of cells can be well approximated with segments of a particular ellipse.
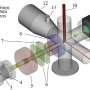
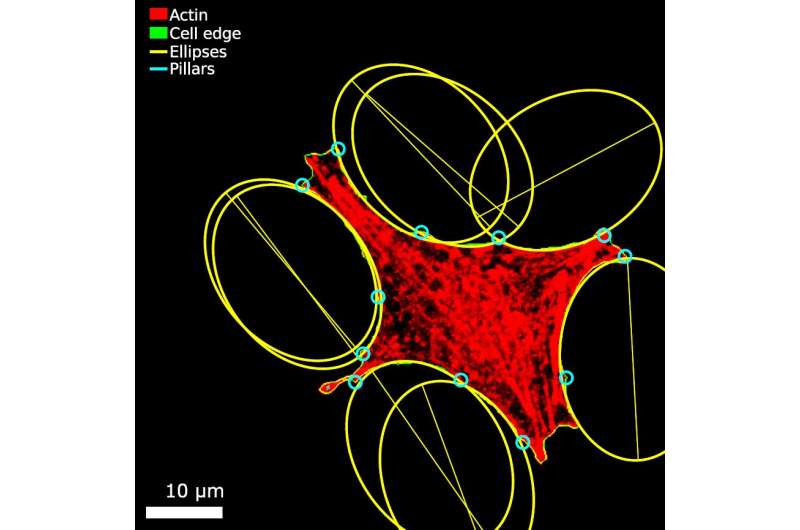
The experimental group of Schmidt imaged the cytoskeleton of a fibroblast cell (see figure) to get a snapshot of its shape. The cytoskeleton is a gel-like material made of small contractile fibers that simultaneously allow cells to keep their structural integrity and exert forces. Meanwhile, the theoretical group of Giomi performed calculations to find out that the curvy shapes around the edge of the cell are parts of one and the same ellipse. Earlier it was assumed that these shapes are part of circles—an assumption that still holds for less mobile cells. The strength of the cells' contractile force dictates the ellipse's eccentricity—or slenderness. When the researchers plotted an ellipse on the actual image, their theory turned out to hold experimentally. What's more, the ellipse's semi-major axis always points in the same direction as the cytoskeletal fibers, also in agreement with the theory.
"Circles have no direction, but ellipses do," says PhD student and co-lead author Koen Schakenraad. "So we have found a clue to explain a cell's sense of direction." The discovery is primarily important to fundamental science. In the long run however, the research field could provide vital insights to the medical sector. Schakenraad: "For instance, a major problem with cancer is metastasis. If we understand how metastases have a sense of direction while spreading, this might provide some insight in cancer research."
More information: Wim Pomp, Koen Schakenraad, Hayri E. Balcioglu, Hedde van Hoorn, Erik H. J. Danen, Roeland M. H. Merks, Thomas Schmidt and Luca Giomi, 'Cytoskeletal anisotropy controls geometry and forces of adherent cells', Physical Review Letters. arxiv.org/abs/1702.03916
Journal information: Physical Review Letters
Provided by Leiden Institute of Physics