Scientists find holes in light by tying it in knots
A research collaboration including theoretical physicists from the University of Bristol and Birmingham has found a new way of evaluating how light flows through space—by tying knots in it.
Laser light may appear to be a single, tightly focused beam. In fact, it's an electromagnetic field, vibrating in an ellipse shape at each point in space. This multidirectional light is said to be 'polarised'.
The effect can be seen with polarised sunglasses, which only allow one direction of light to penetrate. By holding them up to the sky and rotating them, viewers will see darker and brighter patches as light flowing in different directions appears and disappears.
Now, scientists have been able to use holographic technology to twist a polarised laser beam into knots.
Professor Mark Dennis, from the University of Bristol's School of Physics and University of Birmingham's School of Physics and Astronomy, led the theoretical part of the research.
He said: "We are all familiar with tying knots in tangible substances such as shoelaces or ribbon. A branch of mathematics called 'knot theory' can be used to analyse such knots by counting their loops and crossings.
"With light, however, things get a little more complex. It isn't just a single thread-like beam being knotted, but the whole of the space or 'field' in which it moves.
"From a maths point of view, it isn't the knot that's interesting, it's the space around it. The geometric and spatial properties of the field are known as its topology."
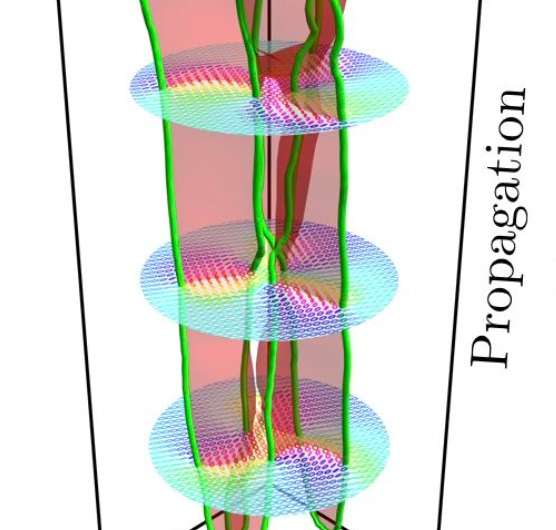
In order to analyse the topology of knotted light fields, researchers from universities in Bristol, Birmingham, Ottowa and Rochester used polarised light beams to create structures known as 'polarisation singularities'.
Discovered by Professor John Nye in Bristol over 35 years ago, polarisation singularities occur at points where the polarisation ellipse is circular, with other polarisations wrapping around them. In 3 dimensions, these singularities occur along lines, in this case creating knots.
The team were able to create knots of much greater complexity than previously possible in light and analysed them in fine detail.
Professor Dennis added: "One of the purposes of topology is to talk about showing data in terms of lines and surfaces. The real-world surfaces have a lot more holes than the maths predicted."
More information: Hugo Larocque et al. Reconstructing the topology of optical polarization knots, Nature Physics (2018). DOI: 10.1038/s41567-018-0229-2
Journal information: Nature Physics
Provided by University of Bristol