Scientists discover the secret behind the stability of carbon isotopes
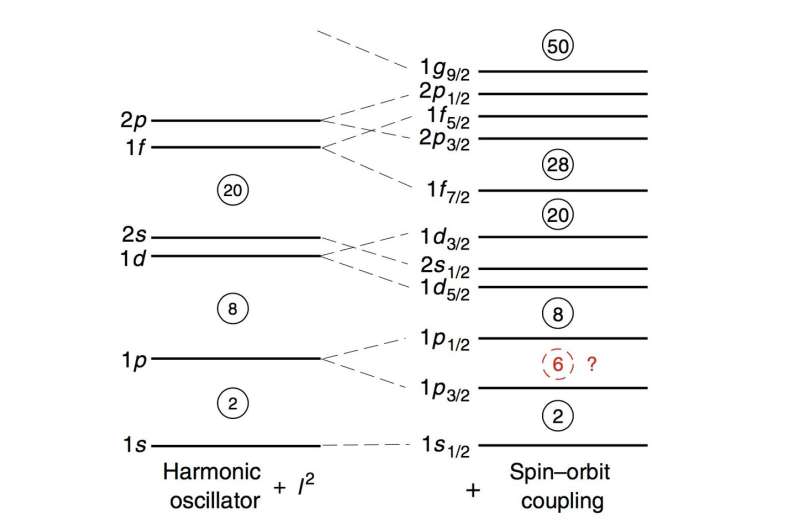
A magic number is a number of protons or neutrons in the nucleus of an atom that results in much greater stability than that of nuclei with other numbers of protons or neutrons.
The magic numbers of nuclei are partly determined by the spin–orbit coupling force, which is related to the spins of the protons or neutrons in a nucleus. The spin–orbit coupling force was introduced by Nobel Laureates Maria Goeppert Mayer and J. Hans D. Jensen in 1949 to explain the splittings of quantum states of protons or neutrons. Its actual nuclear force origin is still not fully understood.
Researchers have identified that the magic number of six is particularly important because it should allow the origin of spin–orbit coupling to be thoroughly investigated. However, the existence of an atomic species with a magic number of six had not been confirmed.
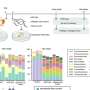
Now, an international research team led by Osaka University has changed this situation by identifying a species of carbon—an essential element for life—that possesses a proton magic number of six. They conducted experiments that allowed them to measure the radii of protons in the nuclei of different carbon isotopes (isotopes have the same number of protons but different numbers of neutrons in their nuclei). Interestingly, the different carbon isotopes displayed very similar proton radii. They published their findings in Nature Communications.
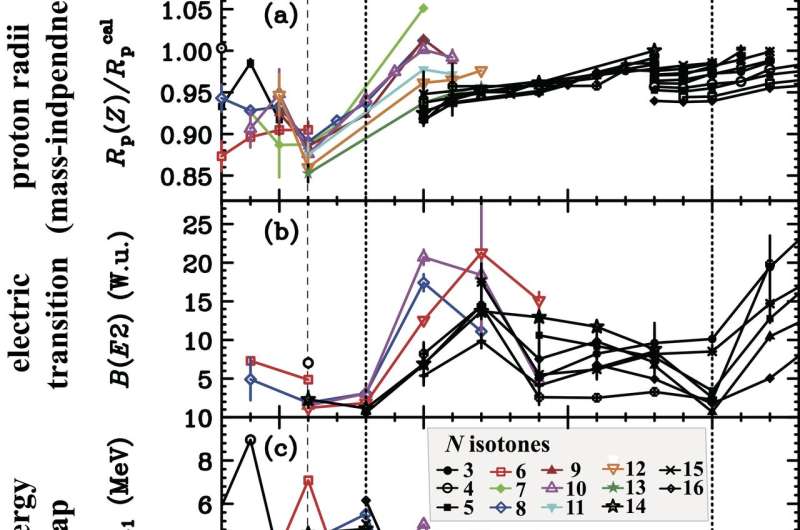
"Combining our radii measurement results with nuclear charge radii, electric quadrupole transition rates, and atomic mass data allowed us to identify a carbon isotope with a predominant magic number of six" study first author Dinh Trong Tran says.
To help understand the experimental results, the researchers conducted computational calculations. Calculated proton radii agreed well with experimental values. The spin–orbit splitting of the carbon isotopes was also investigated by analysis of experimental and theoretical data for the energy to add or remove a proton from the nucleus of each isotope.
"Our analysis clearly demonstrated that large spin–orbit splittings exist universally for atomic nuclei," corresponding author Hooi Jin Ong explains. "In addition, the magic number of six is as prominent as that of other identified magic numbers."
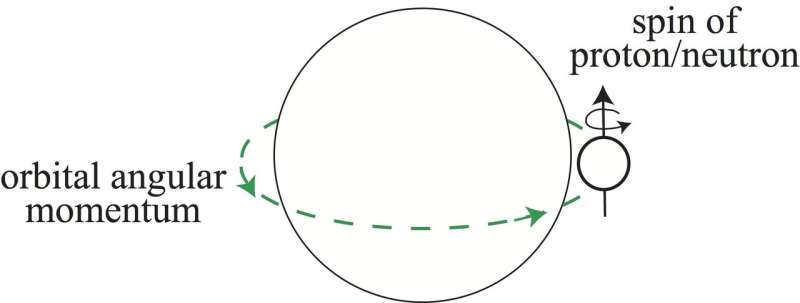
The identification of the magic number of six provides an avenue to investigate the origin of spin–orbit splittings in atomic nuclei. The team's findings increase fundamental knowledge of the spin–orbit force, the origin of the magic number of nuclei, and nucleus stability, representing a contribution to eventual comprehensive understanding of nuclear physics.
More information: D. T. Tran et al. Evidence for prevalent Z = 6 magic number in neutron-rich carbon isotopes, Nature Communications (2018). DOI: 10.1038/s41467-018-04024-y
Journal information: Nature Communications
Provided by Osaka University