Turning entanglement upside down

A team of physicists from ICTP-Trieste and IQOQI-Innsbruck has come up with a surprisingly simple idea to investigate quantum entanglement of many particles. Instead of digging deep into the properties of quantum wave functions, which are notoriously hard to experimentally access, they propose to realize physical systems governed by the corresponding entanglement Hamiltonians. By doing so, entanglement properties of the original problem of interest become accessible via well-established tools.
Quantum entanglement forms the heart of the second quantum revolution: it is a key characteristic used to understand forms of quantum matter, and a key resource for present and future quantum technologies. Physically, entangled particles cannot be described as individual particles with defined states, but only as a single system. Even when the particles are separated by a large distance, changes in one particle also instantaneously affect the other particle(s). The entanglement of individual particles—whether photons, atoms or molecules—is part of everyday life in the laboratory today. In many-body physics, following the pioneering work of Li and Haldane, entanglement is typically characterized by the so-called entanglement spectrum: it is able to capture essential features of collective quantum phenomena, such as topological order, and at the same time, it allows to quantify the 'quantumness' of a given state—that is, how challenging it is to simply write it down on a classical computer.
Despite its importance, the experimental methods to measure the entanglement spectrum quickly reach their limits—until today, these spectra have been measured only in few qubits systems. With an increasing number of particles, this effort becomes hopeless as the complexity of current techniques increases exponentially.
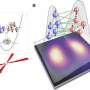
"Today, it is very hard to perform an experiment beyond few particles that allows us to make concrete statements about entanglement spectra," explains Marcello Dalmonte from the International Centre for Theoretical Physics (ICTP) in Trieste, Italy. Together with Peter Zoller and Benoît Vermersch at the University of Innsbruck, he has now found a surprisingly simple way to investigate quantum entanglement directly. The physicists turn the concept of quantum simulation upside down by no longer simulating a certain physical system in the quantum simulator, but directly simulating its entanglement Hamiltonian operator, whose spectrum of excitations immediately relates to the entanglement spectrum.
"Instead of simulating a specific quantum problem in the laboratory and then trying to measure the entanglement properties, we propose simply turning the tables and directly realizing the corresponding entanglement Hamiltonian, which gives immediate and simple access to entanglement properties, such as the entanglement spectrum," explains Marcello Dalmonte. "Probing this operator in the lab is conceptually and practically as easy as probing conventional many-body spectra, a well-established lab routine."
Furthermore, there are hardly any limits to this method with regard to the size of the quantum system. This could also allow the investigation of entanglement spectra in many-particle systems, which is notoriously challenging to address with classical computers. Dalmonte, Vermersch and Zoller describe the radically new method in a current paper in Nature Physics and demonstrate its concrete realization on a number of experimental platforms, such as atomic systems, trapped ions and also solid-state systems based on superconducting quantum bits.
More information: M. Dalmonte et al, Quantum simulation and spectroscopy of entanglement Hamiltonians, Nature Physics (2018). DOI: 10.1038/s41567-018-0151-7
Journal information: Nature Physics
Provided by University of Innsbruck