November 29, 2017 feature
Physicists set new record with 10-qubit entanglement
(Phys.org)—Physicists have experimentally demonstrated quantum entanglement with 10 qubits on a superconducting circuit, surpassing the previous record of nine entangled superconducting qubits. The 10-qubit state is the largest multiqubit entangled state created in any solid-state system and represents a step toward realizing large-scale quantum computing.
Lead researcher Jian-Wei Pan and co-workers at the University of Science and Technology of China, Zhejiang University, Fuzhou University, and the Institute of Physics, China, have published a paper on their results in a recent issue of Physical Review Letters.
In general, one of the biggest challenges to scaling up multiqubit entanglement is addressing the catastrophic effects of decoherence. One strategy is to use superconducting circuits, which operate at very cold temperatures and consequently have longer qubit coherence times.
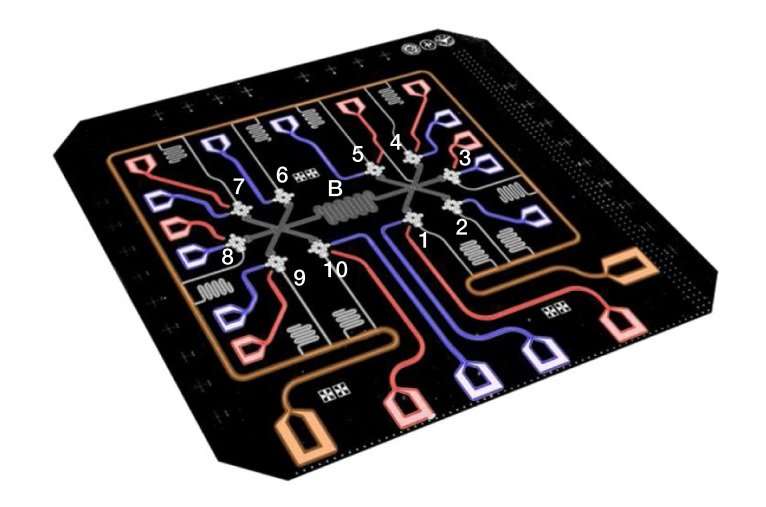
In the new set-up, the researchers used qubits made of tiny pieces of aluminum, which they connected to each other and arranged in a circle around a central bus resonator. The bus is a key component of the system, as it controls the interactions between qubits, and these interactions generate the entanglement.
As the researchers demonstrated, the bus can create entanglement between any two qubits, can produce multiple entangled pairs, or can entangle up to all 10 qubits. Unlike some previous demonstrations, the entanglement does not require a series of quantum logic gates, nor does it involve modifying the physical wiring of the circuit, but instead all 10 qubits can be entangled with a single collective qubit-bus interaction.
To measure how well the qubits are entangled, the researchers used quantum tomography to determine the probability of measuring every possible state of the system. Although there are thousands of such states, the resulting probability distribution yielded the correct state about 67% of the time. This fidelity is well above the threshold for genuine multipartite entanglement (generally considered to be about 50%).
In the future, the physicists' goal is to develop a quantum simulator that could simulate the behavior of small molecules and other quantum systems, which would allow for a more efficient analysis of these systems compared to what is possible with classical computers.
More information:
Chao Song et al. "10-Qubit Entanglement and Parallel Logic Operations with a Superconducting Circuit." Physical Review Letters. DOI: 10.1103/PhysRevLett.119.180511
Also at arXiv:1703.10302 [quant-ph]
Journal information: Physical Review Letters
© 2017 Phys.org