A scalable deep learning approach for massive graphs
A graph structure is extremely useful for predicting properties of its constituents. The most successful way of performing this prediction is to map each entity to a vector through the use of deep neural networks. One may infer the similarity of two entities based on the vector closeness. A challenge for deep learning, however, is that one needs to gather information between an entity and its expanded neighborhood across layers of the neural network. The neighborhood expands rapidly, making computation very costly. To resolve this challenge, we propose a novel approach, validated through mathematical proofs and experimental results, that suggest that it suffices to gather the information of only a handful of random entities in each neighborhood expansion. This substantial reduction in neighborhood size renders the same quality of prediction as state-of-the-art deep neural networks but cuts training cost by orders of magnitude (e.g., 10x to 100x less computation and resource time), leading to appealing scalability. Our paper describing this work, "FastGCN: Fast Learning with Graph Convolutional Networks via Importance Sampling," will be presented at ICLR 2018. My co-authors are Tengfei Ma and Cao Xiao.
Complexity of graph analysis
Graphs are universal representations of pairwise relationship. In real-world applications, they come in a variety of forms, including for example, social networks, gene expression networks, and knowledge graphs. A trending subject in deep learning is to extend the remarkable success of well-established neural network architectures for Euclidean structured data (such as images and texts) to irregularly structured data, including graphs. The graph convolutional network, GCN, is one such excellent example. It generalizes the concept of convolution for images, which may be considered a grid of pixels, to graphs that no longer look like a regular grid.
The idea behind GCN is very simple. Those of us who took Signal Processing 101 or a basic computer vision course are already familiar with the concept of a convolution filter. For images, it is a small matrix of numbers, to be multiplied elementwise with a moving window of the image, with the resulting product-sum replacing the center number of the window. For graphs, this is similar. A good combination of the filters may detect primitive local structures, such as lines in different angles, edges, corners, and spots of a certain color. For graphs, convolutions are similar. Imagine that each graph node is initially attached with a vector. For each node, the vectors of the neighbors are summed (with certain weights and transforms) into it. Hence, all the nodes are simultaneously updated, performing a layer of forward propagation. Graph convolutions may be used to propagate information through neighborhoods so that global information is disseminated to each graph node.
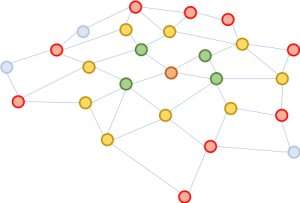
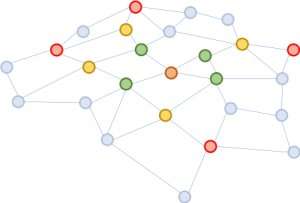
The problem of GCN is that for a network with multiple layers, the neighborhood is quickly expanded, involving many vectors to be summed together, for even just one single node. Such a computation is prohibitively costly for graphs with a large number of nodes. How large will an expanded neighborhood look like? In social network analysis, there is a famous concept coined "six degrees of separation," which states that one may reach any other person on the Earth through six intermediate connections! Figure 1 illustrates that starting from the brown node in the center, expanding the neighborhood three times (in the order of green, yellow, and red) will touch almost the whole graph. In other words, updating the vector of the brown node alone is troublesome for a GCN with as few as three layers.
Simplifying for scalability
We propose a simple yet powerful fix, called FastGCN. If expanding the neighborhood fully is costly, why not expand on only a few neighbors each time? Figure 2 illustrates the concept. Starting from the brown node, in every expansion we pick a constant number (four) of nodes and sum over the vectors from them only. The sampling substantially reduces the cost for training the neural network, by reducing training time by orders of magnitude on benchmark data sets commonly used by researchers. Yet, predictions remain comparably accurate. The size of these benchmark graphs ranges from a few thousand nodes to a few hundred thousand nodes, confirming the scalability of our method.
Behind this intuitive approach is a mathematical theory for the approximation of the loss function. A layer of the network may be summarized as a matrix multiplication: H'=s(AHW), where A is the adjacency matrix of the graph, each row of H is the vector attached to the nodes, W is a linear transformation of the vectors (also interpreted as the model parameter to be learned), and the rows of H' contains the updated vectors. We generalize this matrix multiplication to an integral transform h'(v)= s(òA(v,u)h(u)W dP(u)) under a probability measure P. Then, the sampling of a fixed number of neighbors in each expansion is nothing but a Monte Carlo approximation of the integral under the measure P. The Monte Carlo approximation yields a consistent estimator of the loss function; hence, by taking the gradient, we can use a standard optimization method (such as stochastic gradient descent) to train the neural network.
An array of deep learning applications
Our approach addresses a key challenge in deep learning for large-scale graphs. It applies to not only GCN but also many other graph neural networks built on the concept of neighborhood expansion, an essential component of graph representation learning. We foresee that the resolution of the challenge in this fundamental data structure—graphs—will be adopted in a wide array of applications, including the analysis of social networks, the deep insight into protein-protein interactions for drug discovery, and the curation and discovery of information in knowledge bases.
More information: FastGCN: Fast Learning with Graph Convolutional Networks via Importance Sampling. arxiv.org/abs/1801.10247
Provided by IBM