How to cut your lawn for grasshoppers

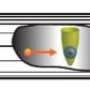
Picture a grasshopper landing randomly on a lawn of fixed area. If it then jumps a certain distance in a random direction, what shape should the lawn be to maximise the chance that the grasshopper stays on the lawn after jumping?
One could be forgiven for wondering what the point of such a question might be. But the solution, proposed by theoretical physicists in the UK and the US, has some intriguing connections to quantum theory, which describes the behaviour of particles at the atomic and sub-atomic scales. Systems based on the principles of quantum theory could lead to a revolution in computing, financial trading, and many other fields.
The researchers, from the University of Cambridge and the University of Massachusetts Amherst, used computational methods inspired by the way metals are strengthened by heating and cooling to solve the problem and find the 'optimal' lawn shape for different grasshopper jump distances. Their results are reported in the journal Proceedings of the Royal Society A.
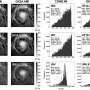
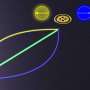
For the mathematically-inclined gardeners out there, the optimal lawn shape changes depending on the distance of the jump. Counter-intuitively, a circular lawn is never optimal, and instead, more complex shapes, from cogwheels to fans to stripes, are best at retaining hypothetical grasshoppers. Interestingly, the shapes bear a resemblance to shapes seen in nature, including the contours of flowers, the patterns in seashells and the stripes on some animals.
"The grasshopper problem is a rather nice one, as it helps us try out techniques for the physics problems we really want to get to," said paper co-author Professor Adrian Kent, of Cambridge's Department of Applied Mathematics and Theoretical Physics. Kent's primary area of research is quantum physics, and his co-author Dr Olga Goulko works in computational physics.
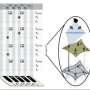
To find the best lawn, Goulko and Kent had to convert the grasshopper problem from a mathematical problem to a physics one, by mapping it to a system of atoms on a grid. They used a technique called simulated annealing, which is inspired by a process of heating and slowly cooling metal to make it less brittle. "The process of annealing essentially forces the metal into a low-energy state, and that's what makes it less brittle," said Kent. "The analogue in a theoretical model is you start in a random high-energy state and let the atoms move around until they settle into a low-energy state. We designed a model so that the lower its energy, the greater the chance the grasshopper stays on the lawn. If you get the same answer - in our case, the same shape - consistently, then you've probably found the lowest-energy state, which is the optimal lawn shape."
For different jump distances, the simulated annealing process turned up a variety of shapes, from cogwheels for short jump distances, through to fan shapes for medium jumps, and stripes for longer jumps. "If you asked a pure mathematician, their first guess might be that the optimal shape for a short jump is a disc, but we've shown that's never the case," said Kent. "Instead we got some weird and wonderful shapes - our simulations gave us a complicated and rich array of structures."
Goulko and Kent began studying the grasshopper problem to try to better understand the difference between quantum theory and classical physics. When measuring the spin - the intrinsic angular momentum - of two particles on two random axes for particular states, quantum theory predicts you will get opposite answers more often than any classical model allows, but we don't yet know how big the gap between classical and quantum is in general. "To understand precisely what classical models do allow, and see how much stronger quantum theory is, you need to solve another version of the grasshopper problem, for lawns on a sphere," said Kent. Having developed and tested their techniques for grasshoppers on a two-dimensional lawn, the authors plan to look at grasshoppers on a sphere in order to better understand the so-called Bell inequalities, which describe the classical-quantum gap.
The lawn shapes which Goulko and Kent found also echo some shapes found in nature. The famous mathematician and code-breaker Alan Turing came up with a theory in 1952 on the origin of patterns in nature, such as spots, stripes and spirals, and the researchers say their work may also help explain the origin of some patterns. "Turing's theory involves the idea that these patterns arise as solutions to reaction-diffusion equations," said Kent. "Our results suggest that a rich variety of pattern formation can also arise in systems with essentially fixed-range interactions. It may be worth looking for explanations of this type in contexts where highly regular patterns naturally arise and are not otherwise easily explained."
More information: The grasshopper problem, Proceedings of the Royal Society A (2017). rspa.royalsocietypublishing.or … .1098/rspa.2017.0494
Journal information: Proceedings of the Royal Society A
Provided by University of Cambridge