How small can superconductors be?

For the first time, physicists have experimentally validated a 1959 conjecture that places limits on how small superconductors can be. Understanding superconductivity (or the lack thereof) on the nanoscale is expected to be important for designing future quantum computers, among other applications.

In 1959, physicist P.W. Anderson conjectured that superconductivity can exist only in objects that are large enough to meet certain criteria. Namely, the object's superconducting gap energy must be larger than its electronic energy level spacing—and this spacing increases as size decreases. The cutoff point (where the two values are equal) corresponds to a volume of about 100 nm³. Until now it has not been possible to experimentally test the Anderson limit due to the challenges in observing superconducting effects at this scale.

In the new study published in Nature Communications, Sergio Vlaic and coauthors at the University Paris Sciences et Lettres and French National Centre for Scientific Research (CNRS) designed a nanosystem that allowed them to experimentally investigate the Anderson limit for the first time.

The Anderson limit arises because, at very small scales, the mechanisms underlying superconductivity essentially stop working. In general, superconductivity occurs when electrons bind together to form Cooper pairs. Cooper pairs have a slightly lower energy than individual electrons, and this difference in energy is the superconducting gap energy. The Cooper pairs' lower energy inhibits electron collisions that normally create resistance. If the superconducting gap energy gets too small and vanishes—which can occur, for example, when the temperature increases—then the electron collisions resume and the object stops being a superconductor.

The Anderson limit shows that small size is another way that an object may stop being a superconductor. However, unlike the effects of increasing the temperature, this is not because smaller objects have a smaller superconducting gap energy. Instead, it arises because smaller crystals have fewer electrons, and therefore fewer electron energy levels, than larger crystals do. Since the total possible electron energy of an element stays the same, regardless of size, smaller crystals have larger spacings between their electron energy levels than larger crystals do.

According to Anderson, this large electronic energy level spacing should pose a problem, and he expected superconductivity to disappear when the spacing becomes larger than the superconducting gap energy. The reason for this, generally speaking, is that one consequence of increased spacing is a decrease in potential energy, which interferes with the competition between kinetic and potential energy that is necessary for superconductivity to occur.

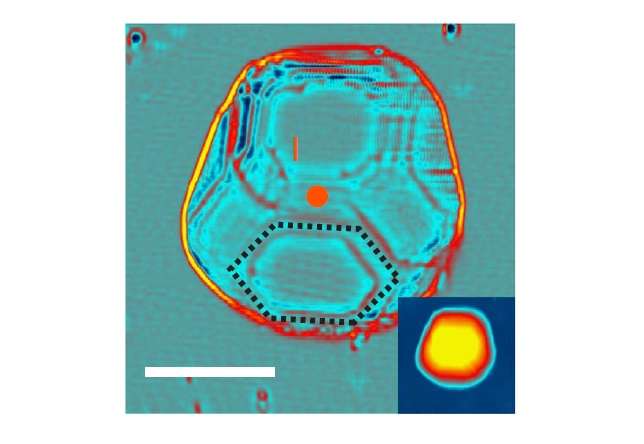
To investigate what happens to the superconductivity of objects around the Anderson limit, the scientists in the new study prepared large quantities of isolated lead nanocrystals ranging in volume from 20 to 800 nm³.

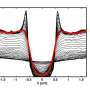
Although they could not directly measure the superconductivity of such tiny objects, the researchers could measure something called the parity effect, which results from superconductivity. When an electron is added to a superconductor, the additional energy is partly affected by whether there is an even or odd number of electrons (the parity), which is due to the electrons forming Cooper pairs. If the electrons don't form Cooper pairs, there is no parity effect, indicating no superconductivity.

Although the parity effect has previously been observed in large superconductors, this study is the first time that it has been observed in small nanocrystals approaching the Anderson limit. In accordance with Anderson's predictions from more than 50 years ago, the researchers observed the parity effect for larger nanocrystals, but not for the smallest nanocrystals below approximately 100 nm³.

The results not only validate the Anderson conjecture, but also extend to a more general area, the Richardson-Gaudin models. These models are equivalent to the conventional theory of superconductivity, the Bardeen Cooper Schrieffer theory, for very small objects.

"Our experimental demonstration of the Anderson conjecture is also a demonstration of the validity of the Richardson-Gaudin models," coauthor Hervé Aubin at the University Paris Sciences et Lettres and CNRS told Phys.org. "The Richardson-Gaudin models are an important piece of theoretical works because they can be solved exactly and apply to a wide range of systems; not only to superconducting nanocrystals but also to atomic nuclei and cold fermionic atomic gas, where protons and neutrons, which are fermions like electrons, can also form Cooper pairs."

On the more practical side, the researchers expect the results to have applications in future quantum computers.

"One of the most interesting applications of superconducting islands is their use as Cooper pair boxes employed in quantum bits, the elemental unit of a hypothetical quantum computer," Aubin said. "So far, Cooper pair boxes used in qubits are much larger than the Anderson limit. Upon reducing the size of the Cooper pair box, quantum computer engineers will eventually have to cope with superconductivity at the Anderson limit."

© 2017 Phys.org