Role of thrust and drag clarified for swimming microorganisms
For years, B. Ubbo Felderhof, a professor at the Institute for Theoretical Physics at Germany's RWTH Aachen University, has explored the mechanisms that fish and microorganisms rely on to propel themselves. Flying birds and insects face similar challenges propelling themselves, but without the luxury of buoyancy these creatures also contend with overcoming gravity to stay aloft.
Over 20 years ago, Felderhof was studying the theory behind the "swimming" of microorganisms, described by the friction interactions between the microbodies and their surrounding fluid. Because of the small mass of many such microorganisms like bacteria, such inertial forces could be neglected in the description. For slightly larger organisms, however, this was not the case.
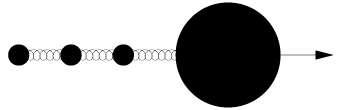
Felderhof has since created mechanical models to more fully develop the theory, consisting of linear chains of spheres connected by springs and immersed in fluid. Here he took into account that the interaction with the fluid involves both friction and inertia, since the effect of mass can't be neglected for these larger structures.
As Felderhof now reports in Physics of Fluids, he's just pushed this work even further by addressing what happens in the case of adding one sphere to the chain that's much larger than the other spheres.
Felderhof studies structures of spheres because the effect of friction and fluid inertia on the motion of a single sphere is fairly well known. With multiple spheres, however, the picture is more complex and has to take into account positions and orientations. "For several spheres, there is the complication of hydrodynamic interactions due to interference of flow patterns," he said. "These hydrodynamic interactions depend on the relative positions of sphere centers."
If the relative positions of the spheres are varied periodically by applying an oscillating force on each of them, with the constraint that the total net force vanishes at any time, the system still sees movement. "In spite of the latter constraint, the set of spheres in general performs a net motion, which is called 'swimming,'" Felderhof said.
A mathematical formulation allows finding the optimum stroke—the combined applied forces—that yields the maximum average speed for a given power.
For this new work, Felderhof explored a linear chain of spheres with one big, passive sphere, meaning the applied force on that sphere vanishes. "The big sphere is called the 'cargo,'" he said. "Think of it as a large body with small moving appendages, or of a boat being pushed or pulled by a small propeller."
His work provides an important conceptual clarification of flow theory. "In popular explanations of swimming and flying, we're told that speed is achieved by a balance of thrust and drag," Felderhof said. "My model calculations, however, show that the mean thrust and drag both vanish when averaged over a period. The effect is more subtle. Interactions of body and fluid are such that periodic shape deformations of the body lead to a net motion relative to the fluid, even though the net thrust vanishes."
Much of the previous work on swimming has concentrated on either the friction-dominated limit, valid for microorganisms, or on the inertia-dominated limit, valid for large animals. "In my model, both friction and inertia play a role so that swimming can be studied in the intermediate regime, where both effects are important," he said.
In terms of applications, the swimming linear chain model is particularly useful because of its slender structure and ability to travel through narrow tubes, such human veins.
"Biologists have already considered the possibility of drug transport via such means," Felderhof said. "And now we've developed a mathematical model that allows optimization of deformations of the body, which leads to maximum speed for given power. This method isn't limited to linear chains, so we can envision applying it to more complicated structures in future work."
First, Felderhof points out that it is important to validate the model by comparison with computer simulations and subsequent experiments, which is beyond his focus, so he hopes other researchers will pursue it.
"Friction and inertia aren't the only effects that can lead to swimming," Felderhof said. "Flapping leads to vortex shedding and possibly a 'street' of vortices. This effect is absent from my model, but may be essential for the swimming of some fish and for flying birds. It will be of value to establish the relative importance of friction, inertia, and vortex shedding, but at present I don't see how this can be accomplished in analytical theory. Again, computer simulation would be helpful."
More information: "Swimming of a nonlinear chain with a cargo in an incompressible viscous fluid with inertia," Physics of Fluids, DOI: 10.1063/1.4973711
Journal information: Physics of Fluids
Provided by American Institute of Physics