May 10, 2016 feature
Geometric heat engine simultaneously maximizes both power and efficiency
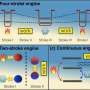
(Phys.org)—As its name suggests, a heat engine converts heat into mechanical energy that can be used to do work—for example, to power a car. Heat engines can operate either in a steady state (where heat is constantly being supplied) or in a cyclic state (where heat is added only during parts of the cycle). Over the past several years, researchers have discovered that steady state heat engines are inherently limited by a power-efficiency trade-off, meaning that their power and efficiency cannot be maximized simultaneously. Although it's not clear if the same is true for cyclic heat engines, some studies have seemed to suggest this to be the case, since operating certain models of cyclic heat engines at slower rates leads to a decrease in power but an increase in efficiency, and vice versa.
Now in a new paper published in Physical Review Letters, Oren Raz and Yigit Subasi from the University of Maryland and Rami Pugatch from the Institute for Advanced Study at Princeton have shown that certain cyclic heat engines do not suffer from a trade-off between power and efficiency like steady state heat engines do. To demonstrate, they designed a cyclic heat engine that can attain both its maximum power and maximum efficiency at the same time.
However, the researchers also showed that cyclic heat engines still have their limits, since it is not possible to design a heat engine that achieves the highest possible theoretical efficiency—the Carnot limit—while producing nonzero power. This limitation is expected, as such a protocol would violate the second law of thermodynamics.
"We showed that, contrary to naïve expectations, power and efficiency can be maximized together and at the fast driving limit," Pugatch told Phys.org. "This does not contradict the laws of thermodynamics since the optimal efficiency in our case is strictly less than Carnot's bound, which is only attainable at slower rates. The question if this has practical meaning depends strongly on the context—but we now showed that such designs are possible, and so maybe clever engineering can harness this to make better engines with a given range of rates."
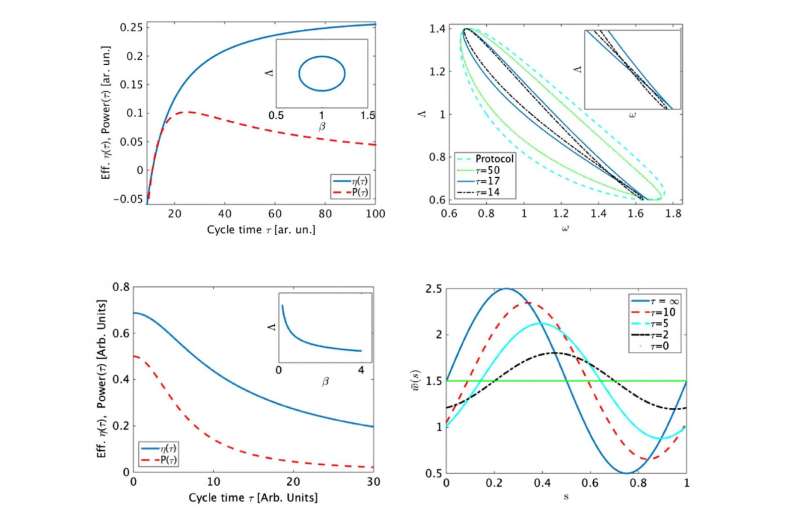
In order to reach these conclusions, the researchers modeled the cyclic heat engine in a new and unusual way: as a "geometric heat engine." From this perspective, the work and heat are interpreted geometrically as areas in state space. The engine's trajectory through this space traces out the area, which determines the work and heat values, during the engine's operating cycle. Larger areas correspond to larger values of work and heat, and the efficiency is defined as the ratio of work to heat.
Modeling the heat engine in this way allowed the researchers to see what happens when work starts to decrease. At these times, the engine's trajectory basically loops around itself so that it temporarily moves in the "wrong" direction, and the area that it traces out in this negatively oriented loop is considered negative. The researchers discovered that a decrease in power and efficiency is associated with a negatively oriented loop in state space.
As the engine drives faster through its cycle, its trajectory changes, and so these areas change their shape. Using this new geometric insight, the researchers were able to design a protocol in which negatively oriented areas never occur, meaning power and efficiency are maximized together as a function of the engine's rate. To do this, they found a set of protocols for which speeding up the driving rate basically closes these detrimental negatively oriented loops that lead to a decrease in power and efficiency. Since increasing the driving rate also "inflates" the area, corresponding to increases in both work and heat, the new protocol achieves both maximum power and maximum efficiency at the fast driving limit.
For now, it's too early to tell exactly how the results could be applied to real engines.
"The results are rather theoretical at the moment, but there are experimental setups that can allow us to test our predicted protocol performance," Pugatch said. "The question if our results are applicable to real engines, for example combustion engines, is open, but for now it seems rather remote too. However, it is our goal to understand how far our general model can be used to predict the performance of real engines, while not succumbing to excessive modeling of any specific combustion engine design."
Although this geometric analysis of cyclic heat engines was used on just two classes of engines, both in a two-dimensional state space, the model might also be extended to higher dimensions. The researchers plan to address this possibility and others in future work.
"There are several extensions we wish to study: first it will be interesting to understand how general our result is, and can our model be used to describe realistic engines, and if not, what are the missing ingredients?" Pugatch said. "Second, we are now studying alternative definitions for engine's efficiency, since we found that the usual definition (work divided by heat extracted) is rather restrictive and that realistic engines often require a modified definition—for example, how much fuel is burned per mile is related but not mathematically equivalent to the usual definition."
More information: O. Raz et al. "Geometric Heat Engines Featuring Power that Grows with Efficiency." Physical Review Letters. DOI: 10.1103/PhysRevLett.116.160601, Also at arXiv:1602.07016 [cond-mat.stat-mech]
Journal information: Physical Review Letters
© 2016 Phys.org