Physicists discover new properties of superconductivity

New findings from an international collaboration led by Canadian scientists may eventually lead to a theory of how superconductivity initiates at the atomic level, a key step in understanding how to harness the potential of materials that could provide lossless energy storage, levitating trains and ultra-fast supercomputers.
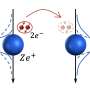
Professor David Hawthorn, Professor Michel Gingras, doctoral student Andrew Achkar, and post-doctoral fellow Dr. Zhihao Hao from University of Waterloo's Department of Physics and Astronomy have experimentally shown that electron clouds in superconducting materials can snap into an aligned and directional order called nematicity.
"It has become apparent in the past few years that the electrons involved in superconductivity can form patterns, stripes or checkerboards, and exhibit different symmetries - aligning preferentially along one direction," said Professor Hawthorn. "These patterns and symmetries have important consequences for superconductivity - they can compete, coexist or possibly even enhance superconductivity. "
Their results, published today in the prestigious journal Science, present the most direct experimental evidence to date of electronic nematicity as a universal feature in cuprate high-temperature superconductors.
"In this study, we identify some unexpected alignment of the electrons - a finding that is likely generic to the high temperature superconductors and in time may turn out be a key ingredient of the problem," said Professor Hawthorn.
Superconductivity, the ability of a material to conduct an electric current with zero resistance, is best described as an exotic state in high temperature superconductors - challenging to predict, let alone explain.
The scientists used a novel technique called soft x-ray scattering at the Canadian Light Source synchrotron in Saskatoon to probe electron scattering in specific layers in the cuprate crystalline structure. Specifically, the individual cuprate (CuO2) planes, where electronic nematicity takes place, versus the crystalline distortions in between the CuO2 planes.
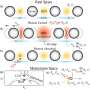
Electronic nematicity happens when the electron orbitals align themselves like a series of rods - breaking their unidirectional symmetry apart from the symmetry of the crystalline structure.
The term "nematicity" commonly refers to when liquid crystals spontaneously align under an electric field in liquid crystal displays. In this case, it is the electronic orbitals that enter the nematic state as the temperature drops below a critical point.
Recent breakthroughs in high-temperature superconductivity have revealed a complex competition between the superconductive state and charge density wave order fluctuations. These periodic fluctuations in the distribution of the electrical charges create areas where electrons bunch up in high- versus low-density clouds, a phenomenon that is now recognized to be generic to the underdoped cuprates.
Results from this study show electronic nematicity also likely occurs in underdoped cuprates. Understanding the relation of nematicity to charge density wave order, superconductivity and an individual material's crystalline structure could prove important to identifying the origins of the superconducting and so-called pseudogap phases.
The authors also found the choice of doping material impacts the transition to the nematic state. Dopants, such as strontium, lanthanum, and even europium added to the cuprate lattice, create distortions in the lattice structure which can either strengthen or weaken nematicity and charge density wave order in the CuO2 layer.
Although there is not yet an agreed upon explanation for why electronic nematicity occurs, it may ultimately present another knob to tune in the quest to achieve the ultimate goal of a room temperature superconductor.
"Future work will tackle how electronic nematicity can be tuned, possibly to advantage, by modifying the crystalline structure," says Hawthorn.
Hawthorn and Gingras are both Fellows of the Canadian Institute For Advanced Research. Gingras holds the Canada Research Chair in Condensed Matter Theory and Statistical Mechanics and spent time at the Perimeter Institute of Theoretical Physics as a visiting researcher while this work was being carried out.
More information: "Nematicity in stripe-ordered cuprates probed via resonant x-ray scattering" Science, DOI: 10.1126/science.aad1824
Journal information: Science
Provided by University of Waterloo