Higgs transition of north and south poles of electrons in a magnet
Minimal evidence of a Higgs transition 1 of north and south poles of electron spins was observed in a magnet Yb2Ti2O7 at the absolute temperature 2 0.21 K. A fractionalization of these monopoles from electron spins was observed on cooling to 0.3 K. On further cooling below 0.21 K, the material showed the ferromagnetism to be understood as a superconductivity of monopoles. The work is reported in an online science journal Nature Communications on August 7, by an international collaboration team.
Electrons rotate like the earth, acting as tiny magnets called spins in magnetic materials. Usually, these spins form a magnetic order on cooling, and the monopoles, namely, north and south poles of electron spins, are confined to each other. In magnetic materials called spin ice 3, the spins remain unordered even at low temperatures, and the monopoles behave as if they are fractionalized while unstable. Since 2010, on the other hand, Dr. Onoda and coworkers have predicted a so-called quantum spin ice 4 that can exhibit a magnetic order realized by a Bose-Einstein condensation of monopoles. In this case, a coupling to fictitious electromagnetic fields, called gauge fields, endows a mass for otherwise gapless spin excitations in the ordered state, forming an analogous superconducting state of monopoles via the Higgs mechanism5. Now, cooling a quantum spin ice material Yb2Ti2O7 to 0.21 K, the team observed a transition from a state with fractionalized unstable monopoles to a ferromagnetic state with condensed stable monopoles, indicating a Higgs transition of monopoles. This state hosting dissipationless monopole current of spins is expected to play important roles in spintronics that aims at efficient controls of magnets for application.
In most of electrically insulating magnets, electrons form tiny magnets called spins by their rotation. A macroscopic number of spins usually show an order at low temperatures, demonstrating a spontaneous symmetry breaking. For instance, in ferromagnets and antiferromagnets, spins show parallel and antiparallel alignments, respectively. However, a geometrical frustration, which will be explained below, sometimes suppresses a formation of the magnetic order, as in materials called spin ice, Dy2Ti2O7 and Ho2Ti2O7.
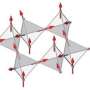
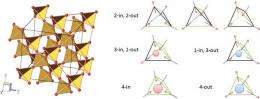
Spins in spin ice are localized at points of a pyrochlore lattice which has a network of corner-sharing tetrahedra (Fig.1, left). Each spin can point only to the "in" or "out" towards the center of the tetrahedron. Two adjacent spins interact with each other so that they form a pair of "in" and "out". However, it is impossible that all the pairs of adjacent spins on a tetrahedron take such pair of "in" and "out" (Fig.1, right: black lines). Because of this frustration, the four spins on each tetrahedron are compromised to form a "2-in, 2-out" structure, as the most stable one (Fig.1, upper right). This is called the ice rule. Yet a huge number of spin configurations satisfy the ice rule over the crystal, preventing a spin ordering even at low temperatures. Inverting a single spin in the ice-rule state creates a pair of unstable "3-in, 1-out" and "1-in, 3-out" tetrahedra hosting a north pole and a south pole of spins at the center, respectively (Fig.1, middle right). These north/south poles are recognized as monopoles fractionalized from electron spins, whereas they are unstable and disappear eventually.
In 2010-2012, Dr. Onoda and coworkers derived a theoretical model called "quantum spin ice" for magnetic materials like Pr2Zr2O7 and Yb2Ti2O7, where monopoles exhibit a motion obeying the quantum mechanics. It has been shown that in certain cases, monopoles undergo a Bose-Einstein condensation leading to a magnetic order where each spin points to a direction largely tilted from the "in" or "out". Now the collaboration team, cooling a quantum spin ice magnet Yb2Ti2O7, challenged an observation of a transition, from the state with fractionalized but unstable monopoles, to the other having condensed monopoles.
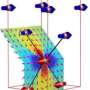
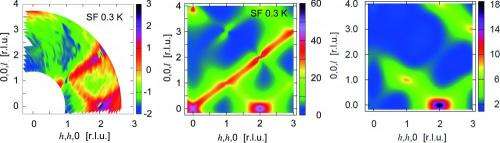
The research team irradiated a neutron beam on the single crystal of Yb2Ti2O7 with the neutron spins being aligned, and then analyzed configurations of electron spins from a pattern of the scattering intensity of neutrons by electron spins. First, the correlation among electron spins was measured at the absolute temperature 0.3 K (Fig.2, left). The result remarkably agrees with a theoretical calculation based on the quantum spin ice model (Fig.2, middle). It reveals such a ridge structure that the scattering intensity strongly depends on the scattering direction, unlike a peak structure to be observed around a transition temperature in conventional magnets (Fig.2, right). This indicates that monopoles become fractionalized from electron spins slightly above the transition temperature in Yb2Ti2O7. Below 0.21 K, a typical scattering pattern indicating a magnetic ordering and a total loss of the polarization of the neutron spins were observed, confirming that the material becomes ferromagnetic. It was also found that at 0.03 K, much lower than the transition temperature, ordered spins pointed to directions that were largely rotated from the "in" or "out" allowed for spin ice. This structure of spin ordering coincides with the theoretical calculation on the same quantum spin ice model at absolute zero temperature. These observations point to a transition due to the quantum-mechanics acting on monopoles, from a magnetic Coulomb liquid where monopoles interact with each other through a Coulomb force analogous to the electric Coulomb force, to a ferromagnetic Higgs phase where the monopoles are condensed (Fig.3).
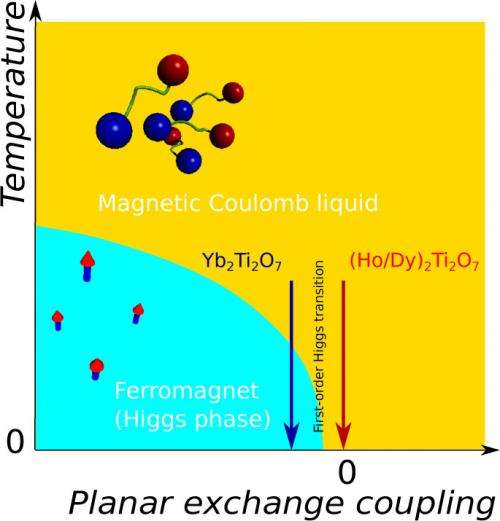
The superconductivity showing zero electric resistivity is used for application. The ferromagnetism in quantum spin ice reported here is expected to provide the spintronics, aiming at efficient controls of the magnetism for device applications, with a new state that can carry monopole current of spins without loss. Quantum spin ice materials, if the Higgs transition temperature is increased to a room temperature, may open a revolutionary industrial engineering.
More information: Lieh-Jeng Chang, Shigeki Onoda, Yixi Su, Ying-Jer Kao, Ku-Ding Tsuei, Yukio Yasui, Kazuhisa Kakurai and Martin Richard Lees. "Higgs transition from a magnetic Coulomb liquid to a ferromagnet in Yb2Ti2O7." Nature Communications 3:992 (2012), DOI: 10.1038/ncomms1989
Journal information: Nature Communications
Provided by RIKEN