July 15, 2014 feature
Particle, meet wave: Optical qubit technique squeezes photons to bridge discrete and continuous quantum regimes
(Phys.org) —While quantum states are typically referred to as particles or waves, this is not actually the case. Rather, quantum states have complementary discrete particlelike and continuous wavelike properties that emerge based on the experimental or observational context. In other words, when used to describe quantum states the terms particle and wave are convenient but inaccurate metaphors. This is an important consideration in quantum computing, where photons are used as units of quantum information known as quantum bits, or qubits, which due to quantum superposition (and therefore unlike classical bits) can simultaneously exist in two states. That said, current attempts to devise quantum computers that process photonic qubits universally using particle detectors to count photons and optical circuits to capture quantum wave evolution have been stymied by the fact that ancilla states – fixed qubit states used in reversible quantum computing as input to a gate to give that gate a more specific logic function – consist of many highly-entangled photons, thereby exceeding experimental capabilities. (Entanglement is a uniquely-quantum state in which two or more interacting particles are said to be hypercorrelated – meaning that the state of each individual particle cannot be described independently, and that a change in a property of one particle is instantly reflected in its entangled partner regardless of the distance separating them.)
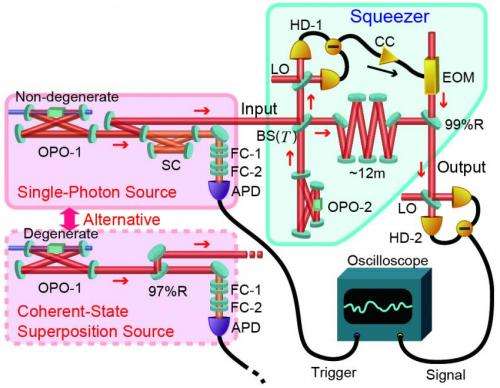
Recently, however, scientists at The University of Tokyo demonstrated for the first time a two-way conversion between a particlelike single-photon state and a wavelike superposition of coherent states by applying quantum squeezing/unsqueezing as a quantum gate, deriving Gaussian (coherent) operations that are applicable to nonclassical, non-Gaussian quantum states and therefore expanding the hybrid quantum-information processing optical toolbox. (In general, a squeezed coherent state is a quantum state in which the uncertainty principle is saturated. Achieved using a number of methods1, squeezed light is a state in which quantum noise is reduced. Specifically, in a squeezed sate the electric field noise paradoxically falls below that of the vacuum state – a phenomenon that has classical counterpart.) Moreover, the researchers say that their so-called squeezing gate will lead to new applications while forming the basis of a new class of optical quantum processors capable of integrating particlelike and wavelike quantum states.
Prof. Akira Furusawa discussed the paper that he and his co-authors published in Physical Review Letters with Phys.org – including the main challenges in successfully applying a quantum optical squeezing operation upon non-Gaussian quantum states, thereby demonstrating a two-way conversion between a particlelike single-photon state and a wavelike superposition of coherent states. "Previous approaches using direct squeezing operations for nonclassical non-Gaussian states were very difficult because such states are very fragile to losses – and direct squeezing operations inevitably have losses," Furusawa tells Phys.org. "In our approach, the squeezing operation is not direct. Instead, we first prepare a squeezed vacuum by using a conventional optical parametric oscillator and then teleport the squeezing operation to fragile nonclassical non-Gaussian states through linear optics, which have almost no losses."
In quantum teleportation2, qubits (specifying, for example, a photon's precise state) are transmitted between quantum-entangled locations via classical communication systems. "In this case, the essential resource is entanglement between the ancillary squeezed vacuum and nonclassical non-Gaussian states, which are created by a beam splitter with no losses," Furusawa notes. "Our successful teleportation of the squeezing operation to a single-photon state and Schrödinger's-cat" – that is, superposition – "state is the first example of deterministic quantum gate teleportation."
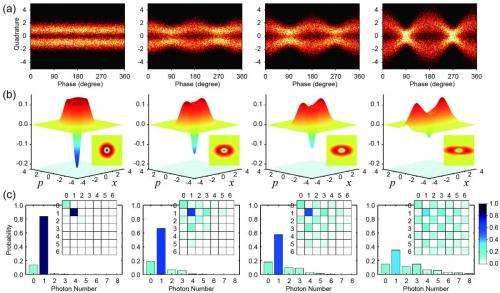
Another first the researchers achieved was using universal and reversible low-loss broadband squeezing to access for the first time a complete set of deterministic Gaussian operations applicable to nonclassical, non-Gaussian states. "A complete set of deterministic Gaussian operations consists of displacement, rotation, and squeezing in phase space," Furusawa explains. "Displacement can be realized by using an optical modulator and a beam splitter, and rotation by controlling optical path length. Therefore, both operations are very easy to apply – even to nonclassical non-Gaussian states.
The last piece of the complete set is squeezing, where we succeeded – also for the first time."
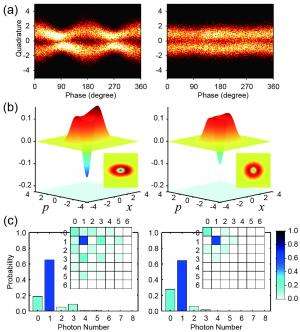
In short, the scientists' key result – demonstrating the very powerful capability of deterministic quantum gate teleportation – allows non-Gaussian operations that can, in principle, be used to build the elusive universal quantum computer. "We want to hybridize the discrete and continuous quantum protocols to build an efficient and robust quantum computer," Furusawa confirms. "The advantage of using qubit protocols is the robustness coming from the digital processing-like finite dimensionality, while the advantage of continuous-variable protocols is efficiency, because they can allow us to make deterministic operations. (Furusawa points out that it remains an open question if this hybridization has implications for ongoing efforts to integrate quantum mechanics and general relativity, which are described using discrete and continuous mathematics, respectively.)
The paper also describes the notable finding that allows the entire Fock space to be used when processing single photons, thereby possibly helping to construct quantum gates and error correction codes for logical qubits. (The Fock space is a mathematical method for articulating the quantum states of a variable, or a non-specified number of identical particles, from a single particle Hilbert space, which is a generalization of Euclidean space.) "Specifically," says Furusawa, "we're now thinking about constructing quantum gates and error correction codes with the hybrid protocol."
Furusawa adds that the deterministic Gaussian operations accessed made possible by their broadband squeezer will directly lead to applications in this area. "Firstly," he illustrates, "we can construct a quantum non-demolition (QND) gate – in which a measured observable's uncertainty does not increase as the quantum system evolve – that corresponds to a qubit controlled NOT (CNOT) gate." Quantum CNOT gates can be used to simulate any quantum circuit to an arbitrary degree of accuracy, as well as to create and dismantle entangled, or EPR (after the 1935 paper3 by Albert Einstein, Boris Podolsky and Nathan Rosen), states. "Secondly, since the QND gate is a universal entangling gate, it allows more complicated quantum gate teleportation."
In addition, Furusawa tells Phys.org, their next target is a particlelike/wavelike hybrid CNOT gate based on non-Gaussian quantum gate teleportation. "We're also thinking about applying this technology to optical communications – especially a quantum mechanically optimal receiver."
More information: Exploring a New Regime for Processing Optical Qubits: Squeezing and Unsqueezing Single Photons, Physical Review Letters 113, 013601 (Published 2 July 2014), doi:10.1103/PhysRevLett.113.013601
Related:
1Squeezed light, arXiv:1401.4118v1 [quant-ph]
2Quantum Teleportation and Entanglement by Akira Furusawa and Peter van Loock, Wiley-VCH (2011), ISBN-13:978-3527409303 (Hardcopy), ASIN:B00BP7S3X8 (Kindle), ISBN:9783527635306 (Google EBook)
3Can Quantum-Mechanical Description of Physical Reality Be Considered Complete? Physical Review 47, 777 (15 May 1935), doi:10.1103/PhysRev.47.777
Journal information: Physical Review Letters
© 2014 Phys.org