October 18, 2013 feature
Feynman wasn't joking: Modeling quantum dynamics with ground state wavefunctions
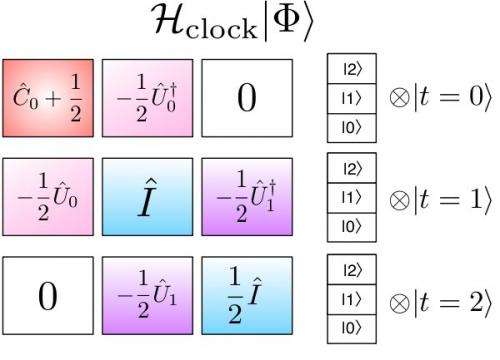
(Phys.org) —Amongst the late Richard Feynman's many prolific and profound contributions to quantum mechanics, the eponymous Feynman clock is perhaps one of the more innovative. Conceived as a solution to the problem of quantum simulation, the Feynman clock proposes using quantum computers to simulate quantum systems – and in so doing, conjectures that if a quantum system moves stepwise forward and then backward in time in equal increments, it would necessarily return to its original state. While originally a linear concept, scientists at Harvard University and the University of Notre Dame recently generalized the proposition to construct a more flexible discrete-time variational principle that leads to a parallel-in-time algorithm. (A variational principle is a scientific principle, used within the calculus of variations, which develops general methods for finding functions which minimize or maximize the value of quantities that depend upon those functions.) The researchers then used that algorithm to describe time-based quantum system evolution as a ground state eigenvalue problem – that is, the quantum system's lowest energy state – which led them to realize that the solution of the quantum dynamics problem could also be obtained by applying the traditional ground state variational principle.
Researcher Jarrod R. McClean discussed with Phys.org the research that he and his colleagues, Profs. John A. Parkhill and Alán Aspuru-Guzik, conducted. "In solving quantum dynamical problems prior to our findings, the large dimension and complexity of models in quantum mechanics make it very computationally expensive to perform dynamics simulations," McClean tells Phys.org. "This means that only very short time scales can be examined with high accuracy. Moreover," he points out, "previous attempts to utilize modern parallel computers have been hindered by strong spatial interactions within quantum systems."
"One usually thinks of quantum information as a field that leads to the development of quantum computers," Harvard's Aspuru-Guzik notes. "It turns out that classical computing can benefit and learn from the ideas of quantum information. This application of Feynman's clock to the challenging problem of time evolution is an example of this."
Traditional algorithms utilize parallelization in space, in which a supercomputer comprising many processors spatially distributes and advances the problem in single temporal increments. "What is less natural," McClean continues, "is to think about the possibility of setting up a calculation that is parallel in time." This means that the simulation at different points in time has to be simultaneously calculated on many processors. "That's the focal point of our study," McClean stresses. "We exploit the clock construction, which was originally designed to think about quantum computing for use in parallel computers."
McClean notes the importance of demonstrating their proposal's accuracy convergence by applying the configuration interaction method – a linear variational method for solving the nonrelativistic Schrödinger equation. "We wanted to show that the convergence of configuration interaction in spacetime has similar properties to its usual application in ground state chemistry," he explains. "To do this, we had to find a system of interest where we could also control the importance of two-body and one-body interactions."
This allowed the researchers to specify a direct analogy to the convergence seen in ground state systems – that is, the rate of expansion convergence is inversely proportional to two-body interaction strength. "As far as we know," McClean says, "nobody has used configuration interaction to do a time-dependent problem in the way we did in our paper."
![The spin triangle within the vanadium compound, used as a model system for the TEDVP. Note that coordinating sodium ions and water molecules are not depicted here. The chemical formula of this compound is given by (CN3H6)4Na2[H4V(IV)6 O8(PO|4)4 (OCH2)3 CCH2OH2] · 14H2O. Credit: Copyright © PNAS, doi:10.1073/pnas.1308069110 Feynman wasn’t joking: Modeling quantum dynamics with ground state wavefunctions](https://scx1.b-cdn.net/csz/news/800a/2013/mccleanfigure2.jpg)
To take advantage of parallel processing in time, McClean notes, the scientists also needed to demonstrate that their construction had a natural division into smaller time segments that could be handled independently by different processors on a parallel computer. "The challenge, of course, was to show that this was computationally advantageous in comparison to traditional approaches of stepping forward in time," he adds.
To address these challenges, McClean says that the key insight at the heart of their work was that tools developed in quantum computation may be exportable to classical simulations of quantum systems. "Through this," he explains, "we recognized that by turning quantum dynamics problems into ground state problems, we could leverage tools from ground state simulation to address difficulties in both the dimension of the space and the length of simulation time required." In addition, he points out that the key to achieving speedup in parallel-in-time algorithms is the ability to precondition, or develop an inexpensive guess for, the solution in serial mode before refining it in parallel mode.
One of the paper's key findings was that the new construction performs favorably against existing algorithms. "We demonstrated that for a representative quantum system, when the same dynamics and partitioning is performed, our algorithm would finish in less human time than the competing algorithms by making use of parallel computer architectures," McClean says. "We ensured that all factors in our comparison were as equal as possible, converging to the same level of accuracy and averaging the speedup results over different time partitions."
McClean acknowledges the possibility of constructing similar algorithms from the other time-dependent variational principles. "However," he points out, "one must be careful when selecting spacetime basis functions. These methods are in their infancy, and it's a current research topic to develop them for use with the Schrodinger equation and quantum mechanics."
In a similar vein, McClean states that there are other methods that use extended spacetime to remove time-dependence from a problem. "However," he clarifies, "these methods use the time-independent Hamiltonian in a way that is similar to traditional time-stepping, retaining many of the drawbacks. In our approach, we take a time-independent construction whose ground state directly encodes the dynamics, allowing us to use any number of previously developed techniques for determining the ground state."
In addition, the metrics inspired by their approach can be used to quantitatively understand the errors resulting from truncating the Hilbert space of many-body quantum dynamics. "In order to make quantum simulations tractable," McClean explains, "it's almost always necessary to hypothesize that a small part of the quantum space is relevant and simulate exclusively in that space. Our metrics allow researchers to quantitatively assess if the selected space includes all the interesting quantum dynamics – and if not, at exactly what time the violation occurs, thereby making it unnecessary to throw out their entire simulation." For example, to simulate the dynamics of charge transfer in a protein, it would be necessary to pick a subset of quantum states and model the dynamics within them. "Our error metrics could allow someone to quickly discover if they had selected the wrong states, and reselect them before too much computational power had been wasted."
In other cases, he continues, the necessary states for simulation might be known, but the total time of simulation needed to see a rare event of interest might be too long for a single processor run in serial . "In that case, our technique could be used in conjunction with spatial parallelization to parallelize over time and reduce the human time required to see that rare event. This leads to faster results and more rapid development of continuing experiments."
Moving forward, McClean believes that there are many untapped resources in the field of quantum information which have the potential to advance classical simulation techniques. "Methods developed for adiabatic quantum computation may be directly applicable to our method to further refine its speed and accuracy. In terms of the planned next steps in their research, he adds that they are looking at applying more advanced techniques from electronic structure to the ground state formulation of dynamics. "Hopefully," he adds, "the methods that have been successful in describing these problems can yield new insights into dynamics problems for quantum chemistry."
McClean notes that there are other areas of research that might benefit from their study. "Our method should be generally applicable across many computational domains that study the time dynamics of physical systems," he tells Phys.org. "While many schemes currently exploit spatial parallelism to take advantage of modern supercomputers, temporal parallelism has been a relatively untapped resource to date. Our method and variations of it," McClean concludes, "will likely be very useful in tapping this additional resource to scale physical simulations to previously unreachable timescales."
More information: Feynman's clock, a new variational principle, and parallel-in-time quantum dynamics, PNAS Published online before print September 23, 2013, doi:10.1073/pnas.1308069110
Journal information: Proceedings of the National Academy of Sciences
© 2013 Phys.org. All rights reserved.











.jpg)







