Researchers discover quantum algorithm that could improve stealth fighter design
(Phys.org) —Researchers at the Johns Hopkins University Applied Physics Laboratory (APL) have devised a quantum algorithm for solving big linear systems of equations. Furthermore, they say the algorithm could be used to calculate complex measurements such as radar cross sections, an ability integral to the development of radar stealth technology, among many other applications. Their research is reported in the June 18 issue of Physical Review Letters.
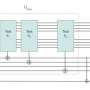
The field of quantum computing is still relatively young. First proposed in the 1980s, a quantum computer harnesses the principles of quantum mechanics (the physics of very small things like electrons and photons) to process information significantly faster than traditional computers. A classical computer has a memory made up of bits (units of information), where each bit represents either a one or a zero. A quantum computer maintains a sequence of qubits. Similar to a bit, a single qubit can represent a one or a zero, but it can also represent any quantum superposition of these two states, meaning it can be both a one and a zero simultaneously.
While several few-qubit systems have been built, a full-scale quantum computer is still years away. Qubits are difficult to manipulate, since any disturbance causes them to fall out of their quantum state or "decohere," and their behavior can no longer be explained by quantum mechanics. Other larger-scale nonuniversal computers have been built—including the much-heralded D-Wave computer, purchased by NASA and Google last month—but none of them currently have the power to replace classical computers.
Theoretical breakthroughs in quantum algorithm design are few and far between. In 1994 Peter Shor introduced a method for finding the prime factors of large numbers—a capability that would render modern cryptography vulnerable. Fifteen years later, MIT researchers presented the Quantum Linear Systems Algorithm (QLSA), which promised to bring the same type of efficiency to systems of linear equations—whose solution is crucial to image processing, video processing, signal processing, robot control, weather modeling, genetic analysis and population analysis, to name just a few applications.
"But it didn't quite deliver; based on their process, no one could figure out how to get a useful answer out of the computer," explains APL's David Clader, who, along with Bryan Jacobs and Chad Sprouse, wrote "Preconditioned Quantum Linear System Algorithm."
As presented, the algorithm had three features that made it dif?cult to apply to generic problem speci?cations and achieve the promised exponential speedup, they wrote. Technical details with setting up the problem on a quantum computer made it unclear how one would apply it to a real-world calculation. In addition, the promise of exponential speedup was only true for a very restricted set of linear systems that typically don't exist in real-world problems. Finally, getting a useful answer from the calculation proved to be quite difficult due to intricacies with the inherently probabilistic nature of quantum measurement.
In their paper, the authors describe how they were able to solve each of these issues and extract useful information from the solution. Furthermore, they demonstrated the applicability of the algorithm by showing how to encode the problem of calculating the electromagnetic scattering cross-section, also known as radar cross section (RCS).
RCS measurements have become increasingly important to the military. It refers to the power that would be returned by an object when illuminated with radar. The power indicates how well the radar can detect or track that target, so there are ongoing efforts to reduce the RCS of such objects as missiles, ships, tanks and aircraft. With a quantum computer, APL researchers have now shown that these calculations can be done much faster and model much more complex objects than would be possible using even the most powerful classical supercomputers.
The work was funded by the Intelligence Advanced Research Projects Activity under its Quantum Computer Science program, which explores questions relating to the computational resources required to run quantum algorithms on realistic quantum computers.
More information: dx.doi.org/10.1103/PhysRevLett.110.250504
Journal information: Physical Review Letters
Provided by Johns Hopkins University










.jpg)