Copper fields: Quantum criticality in high-temperature cuprate superconductors

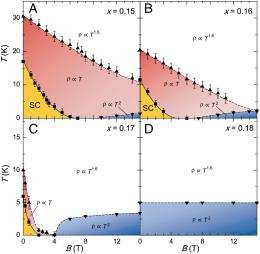
(Phys.org) -- Superconductivity is a complex phenomenon that is considerably more intricate than many casual observers realize. This caveat applies equally to the subset of this research known as high-temperature superconductivity – which, it should be noted, is described as such only in relation to the near absolute zero temperature range at which conventional superconductors are found, and furthermore is not to be confused with the loftier goal of room-temperature superconductivity. That said, certain aspects of electronic properties in high-temperature copper oxide, or cuprate, superconductors imply that the absence of conventional metallic Fermi liquid behavior – the standard model of electrons in metals – and the presence of unconventional superconductivity are closely related. While such a partnership often occurs proximate to what is known as a quantum critical point (a special class of continuous phase transition that takes place at the absolute zero of temperature in a material where the phase transition temperature has been driven to zero by the application of a pressure, field or through doping), the role of quantum criticality in the cuprates has remained elusive. Recently, however, researchers at the Center for Nanophysics and Advanced Materials and Department of Physics, University of Maryland, have studied the anomalous properties of the cuprate material La_2-xCe_xCuO₄, or LCCO, concluding that quantum criticality plays a significant role in shaping the anomalous properties of these superconductive materials.

The research team of Asst. Prof. Johnpierre Paglione faced significant challenges in designing and implementing an experiment to determine the relative importance of quantum criticality in the cuprates. “The relevance of quantum criticality to shaping the properties of the cuprates is a pivotal question that remains unsolved,” Paglione tells Phys.org. “There are several ‘phases’ of these materials, including insulating, anomalous metallic, superconducting and normal metallic ground states – and understanding how these phases arise, coexist, and interact will allow for understanding the underlying physics that gives rise to them.” This is, he adds, the key impetus motivating researchers to understand the phase diagram of the cuprates.

“One of the main challenges in doing so,” Paglione continues, “lies in the fact that there are few actual compounds that can be tuned through the full phase diagram – that is, from parent compound Mott insulator, through the anomalous non-Fermi liquid metallic/superconducting phase, to over-doped ‘normal’ metal. Well-known compounds like yttrium barium copper oxide (YBCO) have a limited range of chemical tuning – by way of oxygen doping or rare earth substitution – which make it difficult to study their properties through all three of these regions of the phase diagram, resulting in the necessity to patch together results from different systems to obtain what is widely held to be the generic cuprate phase diagram.” Luckily, Paglione points out, there are some systems, such as the "hole-doped" (La,Sr)₂CuO₄ and "electron-doped" (La,Ce)₂CuO₄ that allow for a wide range of substitution – and ongoing work has made use of these to answer many questions.

“Another challenge,” Paglione explains, “lies in understanding the details and importance of some of the anomalous normal state properties, that is, above the temperature where superconductivity exists. In particular, most studies to date have focused on the hole-doped cuprates because their superconducting phases exhibit the highest transition temperatures, but these systems all harbor the infamous ‘pseudogap’ phase (a state where the Fermi surface of a material possesses a partial gap) on the underdoped side of the superconducting phase. Much effort has been spent on understanding whether this phase is a ‘friend or foe’ of superconductivity.”

Another issue was that cuprate superconductivity is an amazing phase, having the highest transition temperatures and critical magnetic fields of any known material – but for the purposes of studying the underlying ground state that gives rise to Cooper pairing this is actually a key difficulty. ”Specifically,” Paglione notes, “to study the true ground state properties at the lowest energy scales – those approaching absolute zero – superconductivity must be somehow suppressed. Such high temperatures and fields make it extremely difficult to do high-sensitivity experiments in a practical manner.”

Addressing these issues required no small amount of ingenuity, as well as the particular LCCO compound used in the study. “Firstly,” notes Paglione, “this compound is unique in that it can be synthesized with a wide range of cerium (Ce) concentrations that span across the entire phase diagram, from insulating (x=0) to overdoped metallic (x>0.175). Secondly, this is an electron-doped system, in which the anomalous pseudogap phase is absent. Therefore comparisons of its anomalous properties to those of its hole-doped counterparts with the pseudogap present has allowed us to identify traits common to both, and therefore not associated with the pseudogap phase.”

This includes, most importantly, the linear-in-temperature normal state resistivity that surrounds the superconducting phase. “We can now associate this anomalous scattering with the presence of well-characterized magnetic fluctuations that are almost magnetically ordered, giving strong reinforcement to the well-known hypothesis of quantum critical fluctuations dominating the properties of the normal state,” Paglione explains.

The lower transition temperatures and critical fields of this system allowed the team to probe the ground state in their lab using high but practically attainable extremes of temperature (0.020 Kelvin) and magnetic field (17 Tesla). “With this, we discovered a striking quantum critical scaling of the physical properties with the ratio of temperature to field, which is not seen in a normal metal due to an upper energy scale of the electron system – the Fermi energy – that dominates all characteristics of the metal, such that the normally static factor of temperature is now dynamic. This is a telltale sign of quantum criticality.”

In addition, Paglione points out, there are other innovations that might be developed and applied to the current experimental design. “Due to the crystallographic nature of the LCCO system, it is only stable in thin-film form and therefore single-crystalline samples cannot be synthesized easily.” This is a drawback, since further study of the thermodynamic properties of the system – such as heat capacity and magnetization, which require more sample mass to detect – in the quantum critical regime would allow further insight into its physical description and origin. “Higher magnetic fields and even lower temperatures would allow us to extend the range of applicability of the anomalous properties and therefore further elucidate the extent to which standard model solid state physics fails to explain these materials,” says Paglione.

Relatedly, the team has already defined the next steps to be applied to their research. “Currently we’re most interested in observing the same phenomena in other cuprate materials, allowing for more general conclusions to be made. In particular,” Paglione illustrates, “the similarities of the overdoped side of the phase diagram between hole- and electron-doped cuprates are striking, and they carry a strong potential statement about what governs the demise of superconductivity with increasing doping but require further verification in different compounds.”

One particularly interesting outcome of the study is how the team’s findings impact the development of using the selective response of spin fluctuations and superconductivity to magnetic fields and charge doping to segregate the resulting two distinct signatures of criticality. “The observation of two distinct signatures of quantum criticality is an interesting find. We expected to see only one signature of critical magnetic fluctuations, as given by one set of critical exponents, since an incipient magnetic order and its strong quantum fluctuations are what most people believe lies ‘underneath the dome’ and drives the Cooper pairing. The observation of a second flavor of quantum fluctuations, which we conclude arises from the demise of the superconducting transition temperature to absolute zero, suggests that fluctuations of this separate type of order – that is, superconducting, not magnetic – can also cause anomalous physical properties to arise. These may in fact be the cause of most properties associated with the overdoped side of the phase diagram, including the suppression of superconductivity itself and the strong tuning of the eventual normal metal Fermi liquid ground state.”

Paglione points out that a theory exists for this type of superconducting fluctuation, but a calculation of the expected transport properties has not been done. However, he adds that they are working with Prof. Galitski at the University of Maryland to do just this.

Finally, Paglione explains, there are other research areas and applications that might benefit from their findings. “The study of quantum criticality is a wide field of research that overlaps with superconductivity in several areas, including the cuprates but also in heavy-fermion systems and the more recent discovery of superconductivity in iron-based materials. Our results have implications for all of these areas, where a strong interplay of superconductivity and magnetism results in an easily tunable phase diagram of the sort found in the cuprates. Beyond that,” he concludes, “a deeper understanding of high-temperature superconductivity in cuprates and iron-pnictides has the potential to allow for crystallographic engineering of new compounds that could harbor even higher superconducting transition temperatures useful for room temperature power, electronic and communications applications.”

Copyright 2012 Phys.org
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.