January 4, 2012 feature
Leonardo da Vinci's tree rule may be explained by wind
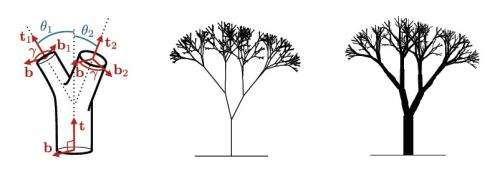
(PhysOrg.com) -- More than 500 years ago, Leonardo da Vinci observed a particular relationship between the size of a tree’s trunk and the size of its branches. Specifically, the combined cross-sectional areas of a tree’s daughter branches are equal to the cross-sectional area of the mother branch. However, da Vinci didn’t know why tree branching followed this rule, and few explanations have been proposed since then. But now in a new study, physicist Christophe Eloy from Aix-Marseille University in Aix-en-Provence, France, has shown that this tree structure may be optimal for enabling trees to resist wind-induced stresses.
In his study, which is published in a recent issue of Physical Review Letters, Eloy explains that Leonardo’s rule is so natural to the eye that it is often used in computer-generated trees. Although researchers have previously proposed explanations for the rule based on hydraulics or structure, none of these explanations have been fully convincing. For instance, the hydraulic explanation called the “pipe model” proposes that the branching proportions have to do with the way that vascular vessels connect the tree’s roots to its leaves to provide water and nutrients. But since vascular vessels account for as little as 5% of the branch cross section (for large trunks in some tree species), it seems unlikely that they would govern the tree’s entire architecture.
“The usual textbook explanation for Leonardo's rule (and, more generally, for the relation between branch diameters) involves hydraulic considerations,” Eloy said. “My study shows that an alternative explanation can be given by considering external loads, such as wind-induced forces.”
Eloy has proposed that Leonardo’s rule is a consequence of trees adapting their growth to optimally resist wind-induced stresses. It’s well-known that plants can alter their growth patterns in response to mechanical sensation, such as wind. The phenomenon, called “thigmomorphogenesis,” means that wind can influence the trunk and branch diameters of a tree as its growing. The underlying cellular mechanisms of this phenomenon are largely unknown.
Building on this line of thinking, Eloy used two models to predict the probability of a fracture at a certain point in a tree due to strong winds. He found that, when the probability of fracture is the same everywhere on the tree, so that each part bears the stress equally, Leonardo’s rule is recovered. He also showed that the diameters of each branch on a tree can be calculated by knowing the parameters of a simple tree skeleton.
Although some of the most common tree species, such as maples and oaks, seem to follow Leonardo’s rule, there are many species that don’t follow the rule, and many more that scientists have yet to analyze.
“Actually, Leonardo’s rule has not been assessed for that many species,” Eloy said. “So far, it seems to be hold for about 10 species. The problem is that it takes a lot of time to measure a single tree, which has thousands of branches, and the data are usually very scattered. Besides, some species clearly do not satisfy Leonardo's rule, such as baobabs, koas, and most bushes.”
The finding that trees seem to follow Leonardo’s rule when adapting their growth to tolerate wind-induced stresses could have applications both in nature and technology.
“It has obvious applications to the forestry industry to calculate the yields of tree stands and to evaluate the risks of breakage during storms,” Eloy said. “It could also be applied to manmade branching structures such as antennas.”
He added that there is still much more to understand about tree design, including the self-similarity shared by large trunks and smaller branches.
“I am still working on this subject, in particular to try to relate growth to external loads,” he said. “In other words, I would like to understand the dynamical growth mechanisms that lead to the intricate fractal structures of trees.”
More information: Christophe Eloy. “Leonardo’s Rule, Self-Similarity, and Wind-Induced Stresses in Trees.” Physical Review Letters 107, 258101 (2011). DOI: 10.1103/PhysRevLett.107.258101
Journal information: Physical Review Letters
Copyright 2012 PhysOrg.com.
All rights reserved. This material may not be published, broadcast, rewritten or redistributed in whole or part without the express written permission of PhysOrg.com.