Uncovering Da Vinci's rule of the trees
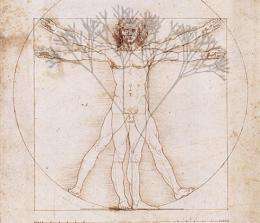
As trees shed their foliage this fall, they reveal a mysterious, nearly universal growth pattern first observed by Leonardo da Vinci 500 years ago: a simple yet startling relationship that always holds between the size of a tree's trunk and sizes of its branches. A new paper has reignited the debate over why trees grow this way, asserting that they may be protecting themselves from wind damage.
"Leonardo's rule is an amazing thing," said Kate McCulloh of Oregon State University, a scientist specializing in plant physiology. "Until recently, people really haven't tested it."
Da Vinci wrote in his notebook that "all the branches of a tree at every stage of its height when put together are equal in thickness to the trunk." In other words, if a tree’s branches were folded upward and squeezed together, the tree would look like one big trunk with the same thickness from top to bottom.
To investigate why this rule may exist, physicist Christophe Eloy, from the University of Provence in France, designed trees with intricate branching patterns on a computer.
"I designed the lightest tree structure to resist wind while still maintaining the strength of the trunk," said Eloy.
Trees are fractal in nature, meaning that patterns created by the large structures, such as the main branches, repeat themselves in smaller structures, such as smaller branches.
Eloy started with a fractal tree skeleton, in which smaller copies of the main branches are repeatedly added together to create the virtual tree. Each new branch takes after its "mother" branch, mimicking the fractal nature of real trees. At this stage, the model tree served merely as a framework for later determining the most effective branch thickness.
Once the skeleton was completed, Eloy put it to the test in a virtual wind tunnel. After applying various wind forces needed to break the branches, Eloy determined the diameters for each branch that limited the chance of snapping. Accounting for every part from the smallest twig to the trunk, the simulation seemed to produce Leonardo's rule.
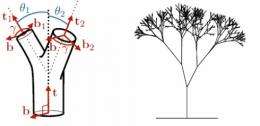
Eloy found that the proportions in his model trees stayed the same regardless of wind speed or the height of the branches, as the rule would predict. His work has been accepted for publication by the journal Physical Review Letters.
Still, some scientists think that there must be more to Leonardo's rule than Eloy's research suggests.
Explanations for the rule generally fall into two categories -- hydrological and structural. Hydrological theories suggest trees have their characteristic shape because it's conducive to efficiently transporting sap, while structural explanations focus on trees' ability to withstand stresses. With his new research, Eloy has bolstered the structural theory.
"I do not doubt that the tree structure is the outcome of a combination of hydraulics and structural constraints," Gil Bohrer, an environmental engineer at Ohio State University in Columbus, told Inside Science in an email. "However, I don't think the hydrological argument should be dismissed so easily."
Regardless of the reason why Leonardo's rule holds, data collected in the field has shown that trees across many species obey the rule. While evidence so far supports the 500-year-old rule, it can be quite tedious to confirm da Vinci's observation.
"The [experimental] data is very scattered," said Eloy. "If you're looking at big trees, there's thousands of branches, and it takes a lot of undergrads to measure it."
Although there's little experimental data to back up da Vinci's observation, his rule has been widely used in computer graphics and mathematical art.
Robert Fathauer -- a physicist and engineer by training turned mathematical artist -- has been exploring the world of fractal trees for years. He uses a process similar to that of Eloy's research to create his artwork.
Fathauer uses a photograph of a single division between a trunk and a branch as the building block for his entire piece. He then repeatedly adds scaled-down versions of the original building block to the outline of a tree. While he doesn't incorporate Leonardo's rule into his work directly, the rule still crops up in his work via the photographs of real trees.
"I did not consciously use [Leonardo's rule] for my art," said Fathauer. "But when I started comparing the surface areas across branchings, I found an experimental verification that Leonardo's rule works pretty well."
Scientists hope further research on this rule will reveal more about wind damage, the structure of forests and the evolution of trees.
"It's exciting that this area is beginning to receive more attention," said McCulloh.
Provided by Inside Science News Service