A 2-dimensional electron liquid solidifies in a magnetic field

The experimental discovery in 1982 of a new Hall conductance step at a fraction ν=1/m with m=3, that is at (1/3)e2/h (with more conductance steps, at other m, found later) – where h is the Planck constant and e is the electron charge – was made for two-dimensional electrons at low temperatures and strong magnetic fields and was greeted with great surprise. The theoretical explanation of this finding a year later by Robert Laughlin in terms of a new form of a quantum fluid, earned him and the experimentalists Horst Störmer and Daniel Tsui the 1998 Nobel Prize with the citation "for the discovery of a new form of quantum fluid with fractionally charged excitations." These discoveries represent conceptual breakthroughs in the understanding of matter, and the fractional quantum Hall effect (FQHE) liquid states, originating from the highly correlated nature of the electrons in these systems, have been termed as new states of matter.

"The quantum fluid state at the 1/3 primary fraction is the hallmark of the FQHE, whose theoretical understanding has been formulated around the antithesis between a new form of quantum fluid and the pinned Wigner crystal," said Landman, Regents' and Institute Professor in the School of Physics, F.E. Callaway Chair and director of the Center for Computational Materials Science (CCMS) at Georgia Tech. "Therefore, the discovery of pinned crystalline signatures in the neighborhood of the 1/3 FQHE fraction, measured as resonances in the microwave spectrum of the two-dimensional electron gas and reported in the Physical Review Letters in September 2010 by a group of researchers headed by Daniel Tsui, was rather surprising," he added.

Indeed, formation of a hexagonally ordered two-dimensional electron solid phase, a so called Wigner crystal (WC) named after the Nobel laureate physicist Eugene Wigner who predicted its existence in 1934, has been anticipated for smaller quantum Hall fractional fillings, ν, of the lowest Landau level populated by the electrons at high magnetic fields, for example ν = 1/9, 1/7 and even 1/5. However, the electrons in the ν=1/3 fraction were believed to resist crystallization and remain liquid.

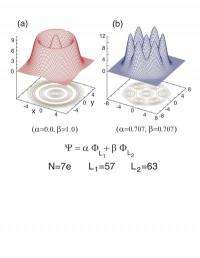
The Georgia Tech physicists developed a theoretical formalism that, in conjunction with exact numerical solutions, provides a unified microscopic approach to the interplay between FQHE liquid and Wigner solid states in the neighborhood of the 1/3 fractional filling. A major advantage of their approach is the use of a single class of variational wave functions for description of both the quantum liquid and solid phases.

"Liquid characteristics of the fractional quantum Hall effect states are associated with symmetry-conserving vibrations and rotations of the strongly interacting electrons and they coexist with intrinsic correlations that are crystalline in nature," Yannouleas and Landman wrote in the opening section of their paper. "While the electron densities of the fractional quantum Hall effect liquid state do not exhibit crystalline patterns, the intrinsic crystalline correlations which they possess are reflected in the emergence of a sequence of liquid states of enhanced stability, called cusp states, that correspond in the thermodynamic limit to the fractional quantum Hall effect filling fractions observed in Hall conductance measurements," they added.

The key to their explanation of the recent experimental observations pertaining to the appearance of solid characteristics for magnetic fields in the neighborhood of the 1/3 filling fraction is their finding that "away from the exact fractional fillings, for example near ν=1/3, weak pinning perturbations, due to weak disorder, may overcome the energy gaps between adjacent good angular momentum symmetry-conserving states. The coupling between these states generates broken-symmetry ground states whose densities exhibit spatial crystalline patterns. At the same time, however, the energy gap between the ground state at ν=1/3 and adjacent states is found to be sufficiently large to prevent disorder-induced mixing, thus preserving its quantum fluid nature."

Furthermore, the work shows that the emergence of the crystalline features, via the pinning perturbations, is a consequence of the aforementioned presence of crystalline correlations in the symmetry-conserving states. Consequently, mixing rules that govern the nature of the disorder-pinned crystalline states have been formulated and tested. Extrapolation of the calculated results to the thermodynamic limit shows development of a hexagonal Wigner crystal with enhanced stability due to quantum correlations.

"In closing, the nature of electrons in the fractional quantum Hall regime continues now for close to three decades to be a subject of great fascination, a research field that raises questions whose investigations can lead to deeper conceptual understanding of matter and many-body phenomena, and a rich source of surprise and discovery," said Landman.

Provided by Georgia Institute of Technology