Extending the uncertainty principle by using an unbounded operator

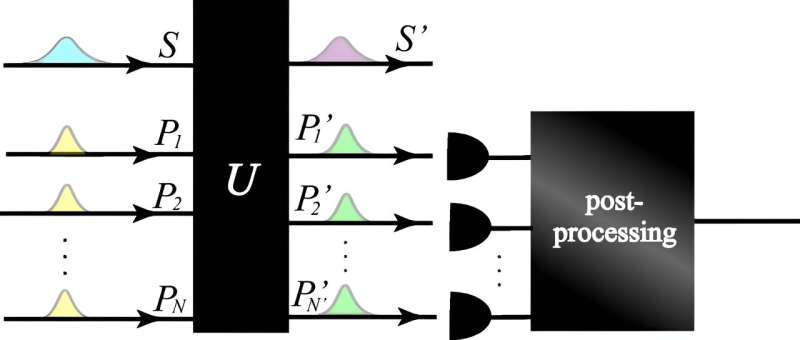
A study published in the journal Physical Review Letters by researchers in Japan solves a long-standing problem in quantum physics by redefining the uncertainty principle.

Werner Heisenberg's uncertainty principle is a key and surprising feature of quantum mechanics, and he can thank his hay fever for it. Miserable in Berlin in the summer of 1925, the young German physicist vacationed on the remote, rocky island of Helgoland, in the North Sea off the northern German coast. His allergies improved, and he was able to continue his work trying to understand the intricacies of Bohr's model of the atom, developing tables of internal atomic properties, such as energy, position and momentum.

When he returned to Göttingen, his advisor, Max Born, recognized these tables could each be formed into a matrix—essentially a two-dimensional table of values. Together with the 22-year-old Pasqual Jordan, they refined their work into matrix mechanics—the first successful theory of quantum mechanics—the physical laws that describe tiny objects like atoms and electrons.

While matrix mechanics would within years be replaced by Schrödinger's wave function and his equation, it did allow Heisenberg the insight to formulate the uncertainty principle: there is a limit to how precisely the location and momentum of a quantum system, typically a particle, can be measured.

The limit of the product of the measurement uncertainties of the two quantities is h/4π, where h is the Planck constant, extremely small but nonetheless not zero. In short, one cannot measure both the position and momentum of a quantum object to arbitrary precision—measuring one to higher precision means the other can only be measured to a lower precision.

In a physical view, suppose we want to measure the position and momentum of an electron. One must shine light of some sort onto a system in order to measure its properties. Light is quantized as photons, which have a nonzero energy. Shining a photon on the electron necessarily disturbs the electron from its original state. In quantum mechanics the mere act of measurement imposes a limit on the precision of the measurement.

Similar uncertainties hold for measurements of time and energy, and angular position and angular momentum, and in general any two variables that do not "commute" when represented as operators in rigorous quantum mechanics.

A few decades later the uncertainty principle was refined by physicists Eugene Wigner, then Huzihiro Araki and Mutsuo M. Yanase into the Wigner-Araki-Yanase (WAY) theorem, which states that for two observable quantities q and p, where p is conserved (such as momentum of a system), then even if p is not measured at all, q cannot be measured with arbitrary precision.

"As a consequence of the WAY theorem we can see that (in a certain sense) it is impossible to measure the particle's position q; all we can measure is its position relative to the apparatus, q—Q," mathematician John Baez of the University of California, Riverside has written, where Q is the position of the measuring apparatus.

But the WAY theorem only applied to quantities like a particles spin, which can only take discrete and bounded quantities.

Now Yui Kuramochi of Kyushu University and Hiroyasu Tajima of the University of Electro-Communications in Japan have solved a long-standing problem by showing that the WAY theorem also applies to observable quantities that are continuous (not discrete) or unbounded, such as position.

"According to the uncertainty principle, position and momentum cannot be accurately measured simultaneously," said Kuramochi. "Our result gives an additional restriction: even only the position itself cannot be measured accurately, as long as we use natural measurements satisfying the momentum conservation." Their proof examines an "unbounded operator," physical quantities that can take infinitely large values.

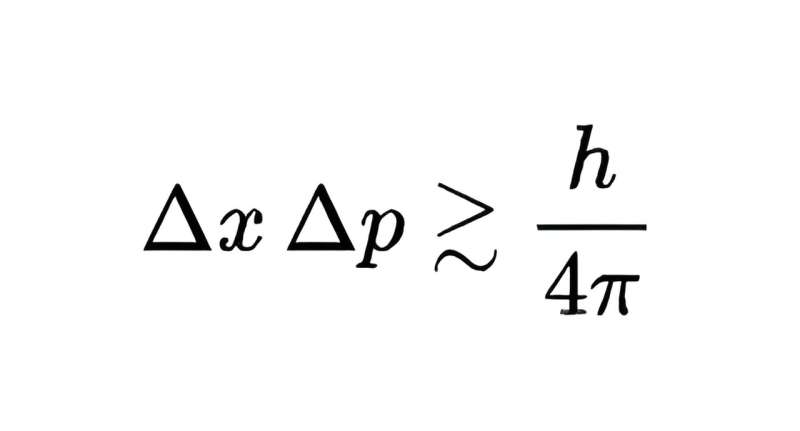
Strictly speaking, the result requires a particular condition that underlies the WAY theorem, called the Yanase condition. While very technical, it essentially stipulates the compatibility of the unbounded variable of the apparatus with the conserved quantity. The Yanase condition, while mathematical, seems desired by applications to real world physical systems.

"The WAY theorem predicts that under a conservation law, a physical quantity that does not commute with the conserved charge cannot be measured without error," Kuramochi continues. "This corresponds to an answer to a 60-year open problem. The new result solves a decades-old problem of how to approach such continuous and unbounded observables, especially in fields like quantum optics, where the new theorem extension is likely to find applications."

The original WAY theorem prohibits the measurement error to be zero, but it is a qualitative theorem and does not specify the measurement limit or even whether there is a lower bound greater than zero. The same applies to this WAY theorem extension by Kuramochi and Tajima.

In their paper the authors write that it is still an open question whether the original WAY theorem for repeated measurements can be generalized as they have, to unbounded conserved observables.

Suggesting new directions of investigation into extensions of the WAY theorem, the team would like to generalize their results to energy-constrained states, as their current results are restricted to state-independent cases, and to approximate cases. One potential application is setting limits on how quantum network transmission protocols can perform better than classical limits.

© 2023 Science X Network