November 15, 2023 feature
This article has been reviewed according to Science X's editorial process and policies. Editors have highlighted the following attributes while ensuring the content's credibility:
fact-checked
peer-reviewed publication
trusted source
proofread
Study resolves puzzles in gravitational collapse of gravitational waves
Black holes are regions in space where the gravitational pull is so strong that nothing can escape them, not even light. These fascinating regions have been the focus of countless studies, yet some of the physics underlying their formation is not yet fully understood.
Black holes are formed in what is known as gravitational collapse. This is essentially the contraction of a cosmological object, prompted by its own gravity drawing matter inward (i.e., toward the object's center of gravity).
Whether or not such a collapsing object forms a black hole depends on the specific properties of the object. In some cases, an object may be very close to the threshold, having a hard time deciding whether or not to form a black hole. This type of collapse results in so-called critical phenomena.
Physicists have been trying to understand critical phenomena in gravitational collapse for decades, as some of its properties are shared by other well-known physical systems. A recent paper published in Physical Review Letters by an international research collaboration based at Bowdoin College in the United States and other institutes in Germany, Prague, the U.K. and Portugal, found agreement among three independently conducted numerical simulations of these phenomena and resolved some long-standing puzzles in this area of study.
"Critical phenomena in gravitational collapse, close to the onset of black-hole formation, were first reported by Matt Choptuik about 30 years ago," Thomas W. Baumgarte, co-author of the paper, told Phys.org.
"In part because these effects share many properties with critical phenomena in other fields of physics (e.g., phase transitions in statistical physics) and in part because they address fundamental questions regarding the properties of general relativity, they immediately caught the attention of many researchers from different fields of physics."
Two of the most fascinating properties of critical gravitational collapse are universality and self-similarity. In this context, the term universality refers to the idea that no matter how a calculation begins, as the onset of a black hole's formation approaches, the solution will always be the same. Self-similarity, on the other hand, means that this universal solution will repeat the same patterns as the physical scale is reduced.
"While Choptuik's calculations involved a so-called scalar field as a matter source, Andrew Abrahams and Chuck Evans soon afterward reported similar effects for the gravitational collapse of gravitational waves (i.e., for pure gravity in the absence of any matter)," Baumgarte explained.
"A further difference is that Choptuik was able to assume spherical symmetry, while gravitational waves cannot exist in spherical symmetry, so that Abrahams and Evans had to relax the assumption of spherical symmetry. Unfortunately, it has been very difficult to reproduce these latter results, as some numerical codes completely failed in this case, or provided results that appeared to contradict those of Abrahams and Evans."
Following the apparently contradictory results obtained in the 1990s, the nature of the critical collapse of "pure gravity" remained an unsolved mystery for almost three decades. Recently, however, three different research groups carried out independent numerical simulations of this collapse, using independently developed codes.
"All these three codes solve Einstein's equations of general relativity, but they use completely different numerical strategies (e.g., spectral methods versus finite-difference methods)," Baumgarte said. "Cartesian coordinates versus spherical polar coordinates, different gauge conditions, etc. All three codes also make different choices for the so-called 'slicing condition' (i.e., they adopt different choices for the rate at which time advances in the codes)."
The key objective of the recent study by Baumgarte and his colleagues was to collectively examine the three numerical simulations that were recently performed by these three different research teams. Their paper was thus a joint effort by the teams, aimed at bridging their independent research efforts to shed new light on the nature of gravitational collapse.
"As a first finding we report that, despite all the numerical differences, our codes produce completely consistent results for the critical collapse of gravitational waves," Baumgarte said. " This gives us confidence that these findings are correct, and not numerical artifacts. Making a suitable choice for the slicing condition turns out to be crucial: a very common other choice, one that has been successful for many other numerical relativity simulations, fails for this case, which explains why some previous attempts to solve this problem failed."
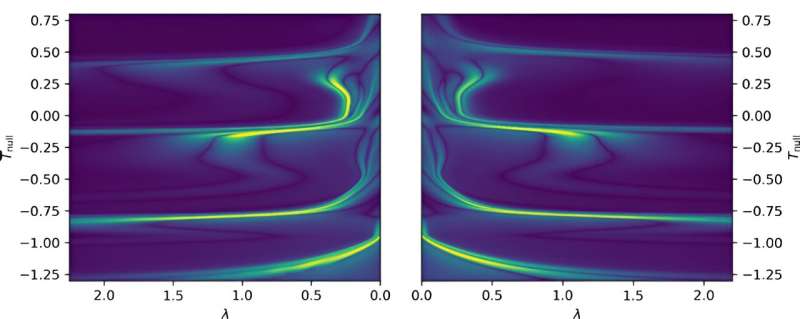
Notably, in their three independent numerical simulations, the researchers found no evidence supporting the property of universality. In other words, they found that starting the numerical with different initial data resulted in different values while approaching the formation of a black hole.
"Our findings explain another piece of the puzzle," Baumgarte said. "Some previous studies had reported differences from the results of Abrahams and Evans, which therefore appeared conflicting, However, those studies also used different initial data. A disagreement between the results therefore constitutes a contradiction only under the assumption of universality—for which we do not see any evidence."
While the researchers found no evidence of universality, they found approximate evidence of self-similarity. Interestingly, however, unlike that observed in the case of critical collapse in spherical symmetry, the self-similarity they observed did not appear to be exact.
Back in the 1990s, Abrahams and Evans had also reported a non-exact self-similarity. These recent results are thus aligned with previous findings, potentially suggesting that reported departures from an exact self-similarity could be linked to the absence of a spherical symmetry.
The recent work by Baumgarte and his colleagues could soon pave the way for new numerical and theoretical studies aimed at further studying and re-framing the critical collapse of gravitational waves. This could bring physicists closer to unveiling the nature and mysteries of this intriguing physical phenomenon, known to precede the formation of black holes.
"While we believe that our work has resolved several open questions in the context of critical collapse of gravitational waves, several follow-up questions remain," Baumgarte added. "For example, we found approximately self-similar solutions for some families of initial data, but not for others, and the nature of the 'threshold solution' for those other families remains unclear.
"It would also be desirable to perform simulations with better fine-tuning to the onset of black-hole formation (e.g., using numerical codes with better resolution and/or other improvements) to explore whether a universal critical solution emerges for fine-tuning that is better than anybody has achieved so far.
"Finally, we plan to investigate what causes the departures from an exact self-similarity and determine if these departures are directly related to the absence of spherical symmetry."
More information: Thomas W. Baumgarte et al, Critical Phenomena in the Collapse of Gravitational Waves, Physical Review Letters (2023). DOI: 10.1103/PhysRevLett.131.181401
Journal information: Physical Review Letters
© 2023 Science X Network