Generalization of the Hall-Petch and inverse Hall-Petch relations

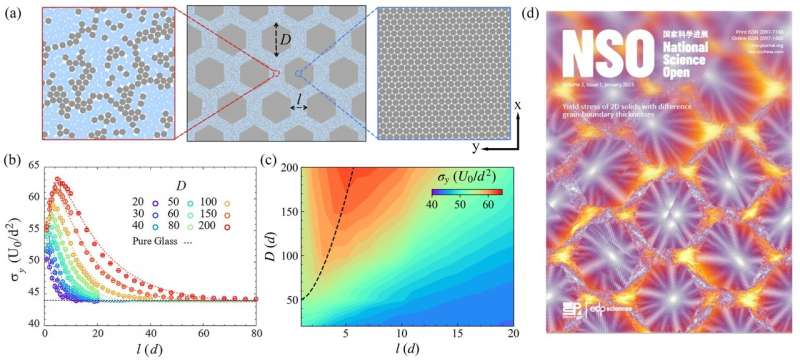
Most crystalline materials are polycrystals, such as metals. They are composed of many small crystalline grains with different lattice orientations. The interface between two crystalline grains, i.e., the grain boundary, is a thin layer of disordered particles about one or two particles thick.

The polycrystal strength increases as the mean grain size decreases, known as the famous Hall-Petch behavior. This trend reverses when the mean grain diameter is below a critical value of 10–15 nanometers (about 50 atoms), i.e., the reverse Hall-Petch behavior. These trends hold for various polycrystals composed of different atoms and molecules.

However, how the strength varies with the thickness of the disordered grain boundary has rarely been asked and poorly understood, probably because polycrystals with thick grain boundaries are not easy to fabricate and control. Although this basic question can be relatively easily explored by computer simulation, related research remains lacking.

In recent years, breakthroughs in the fabrication of crystalline-amorphous composite materials lead to solids with various excellent properties, such as ultrahigh-strength alloys. These solids can be regarded as polycrystals with thick disordered grain boundaries, but the grain-boundary thickness cannot be well controlled and its influence on the material strength remains unclear. Moreover, how to match the grain size and grain boundary thickness to maximize the strength of the material is yet to be explored.

Recently, these questions were studied by Professor Yilong Han of the Department of Physics of the Hong Kong University of Science and Technology (HKUST) and Zhibin Xu, a Ph.D. student of the HKUST Guangzhou Campus, with the participation of Mengmeng Li, a Ph.D. student of the HKUST, and Professor Huijun Zhang of the School of Materials Science and Technology of Xi'an Jiaotong University,

Their computer simulations on 2D solids generalized the material strength from the traditional single-variable function (that is, Hall-Petch and inverse-Hall-Petch relations) to a function with two variables of grain size and grain boundary thickness.

They observed that increasing the thickness of the disordered grain boundaries and decreasing the grain diameter had similar effects on the yield stress, that is the strength, because the proportion of disordered structure was increased in both cases. When the average grain diameter was greater than about 50 particles, as the thickness of the grain boundary increased, the strength of the solid initially increased (that is, the strengthening stage) and then weakened (the weakening stage).

Their corresponding mechanisms were the dislocation gliding within the crystalline grains and deformation within grain boundaries, which were similar to the mechanisms of Hall-Petch and inverse-Hall-Petch relations, respectively. When the grain boundary diameter was less than 50 particles, the plastic deformation was entirely within the grain boundary and thus the strengthening stage was absent.

"We find how to properly thicken the grain boundaries to exceed the maximum strength of traditional polycrystals by systematically measuring the mechanical strength in a more comprehensive 2D parameter space. It can guide the manufacture of higher-strength solids," Zhibin Xu said.

"The relationship between solid structure and material properties is a key topic in material science and mechanical engineering. Much attentions in these fields are paid to the practical problem of how to mix ordered and disordered structures to achieve the maximum strength in real 3D materials, without making analogies or generalization on the classic Hall-Petch and inverse-Hall-Petch relations. We are more curious about the strength or other properties in a more comprehensive parameter space," Yilong Han said.

"Physicists often use simple models to understand general behaviors. Herein we only studied simple 2D solids with Lennard-Jones particle interactions as the first step. The trend of material strength observed in 2D solids should similarly exist in 3D solids because of their similar deformation mechanisms. It is practical to test these results in 3D simulation and experiment in the future."

Moreover, in contrast to the intensively studied liquid-to-glass transition and the direct collapse of single crystal to glass (i.e. amorphous solid), the polycrystal-to-glass transition has rarely been studied. The previous work by Han's group revealed a sharp polycrystal-to-glass transition for the first time by tuning the grain size. Here, tuning grain-boundary thickness is an alternative route to achieve the polycrystal-to-glass crossover, and thus it provides a novel platform for the study of polycrystal-to-glass transition in the future.

The research is published in the journal National Science Open.