Extraction of topological invariants from band structure in the synthetic frequency dimension

Over last few decades, study of topological phases of matter in solid-state electron systems has been extended to other research fields, including synthetic dimensions, and motivates extensive research on topological materials in many systems. Synthetic dimensions in photonics constructed by coupling internal degrees of freedom of light has manifested as a powerful platform for creating synthetic lattices with artificial connectivities.

Synthetic dimensions offer exciting new ways to explore higher-dimensional physics in lower geometrical dimensionality, simplify the setup for achieving unusual functionalities that are hard to be achieved in real space, and manipulate light in multiple ways.

Among them, dynamically modulated ring resonator systems, where resonant modes with equally spaced frequencies are coupled by external modulation to construct a synthetic frequency dimension, can provide great experimental flexibility and reconfigurability to construct more complex lattice structures.

Topological phases of matter play an essential role in many branches of photonics for providing exotic properties, which can be classified by their topological invariants.

For a one-dimensional (1D) system, such as the well-known SSH model, the topology is characterized by the Zak phase, which has been demonstrated within several experimental schemes in photonics. In spite of these progresses, there has been a remarkable challenge that the topological information of conventional 1D SSH model cannot be directly distinguished from the measured band structure in the current photonic or condensed matter platforms due to the identical band shapes for both topological trivial and non-trivial cases.

Study of 1D synthetic SSH model constructed along the frequency dimension of dynamically modulated ring resonators would provide richer physics and new routes to extract topological phase information.

In a new paper published in Light: Science & Applications, a team of scientists, led by Professor Xianfeng Chen and Professor Luqi Yuan from State Key Laboratory of Advanced Optical Communication Systems and Networks, School of Physics and Astronomy, Shanghai Jiao Tong University, China and co-workers for the first time demonstrated a direct experimental measurement of Zak phase from the bulk band structure for a synthetic SSH model by utilizing the frequency axis of light, constructed in two coupled ring resonators by the bichromatic modulations at different amplitudes.

This novel study is enabled by merging topological photonics and band structure analysis in the synthetic frequency dimension and can further promote both fields by introducing a new way for exploring topological phases of matter with experimental feasibility and reconfigurability.

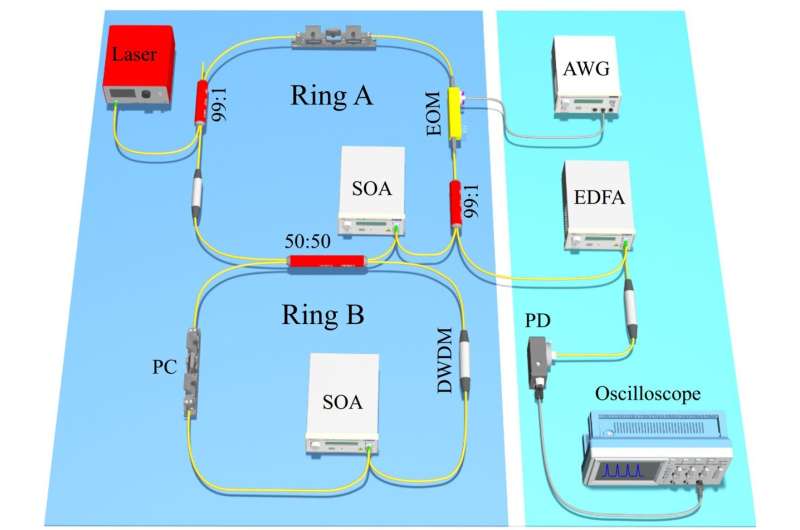
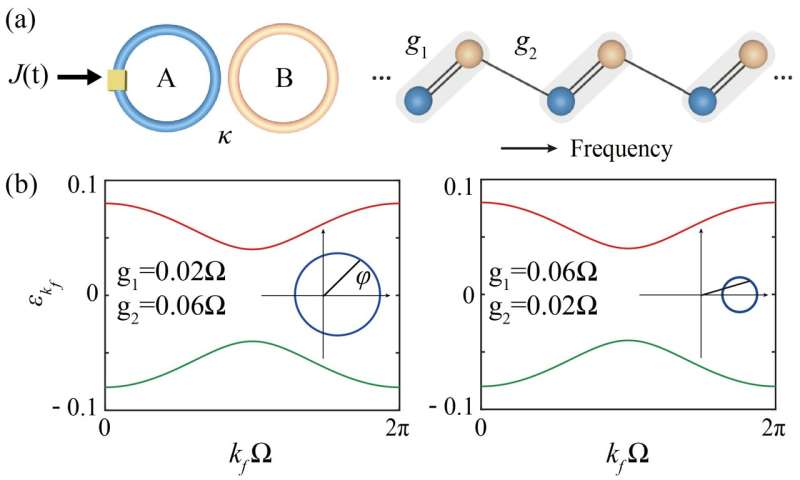
The 1D SSH model along the frequency dimension is constructed by two coupled ring resonators of 10.2 m long. The symmetric and antisymmetric supermodes in the ring resonator system have frequency splitting of 2κ=Ω/3=2π•6.67 MHz (Ω is the free spectral range) and are connected by the electro-optic phase modulator (EOM), which provides bichromatic sinusoidal modulations at different amplitudes. The supermodes act as synthetic lattice sites, with alternating hopping amplitudes g₁ and g₂.

The topologically non-trivial and trivial transmission cases can be converted flexibly by the external modulation. The Zak phase to be measured can be obtained theoretically by integrating the Berry curvature over the first Brillouin zone and take two values, which are 0 for the topologically trivial case and π for the topologically non-trivial case, respectively.

To implement the proposal in the experiment, the projected band structure of the synthetic lattice is obtained through the time-resolved band structure spectroscopy by collecting the drop-port transmission spectrum through the output fiber coupler via linearly scanning the frequency of the input laser source.

A data-analysis scheme called resonant method is applied to extract the geometric phases encoded in the bulk band due to projections of the band structures onto superpositions of the two supermodes with the frequency difference as the lattice sites in the frequency dimension.

The proposal is validated in experiments performed at the telecom wavelength, where distinguishable time-resolved transmission spectra in the non-trivial and trivial phases are obtained. Zak phase values (∼ 0 and 0.98π) are then extracted in different topological phases with a good fit between the simulation results and the experimental measurements.

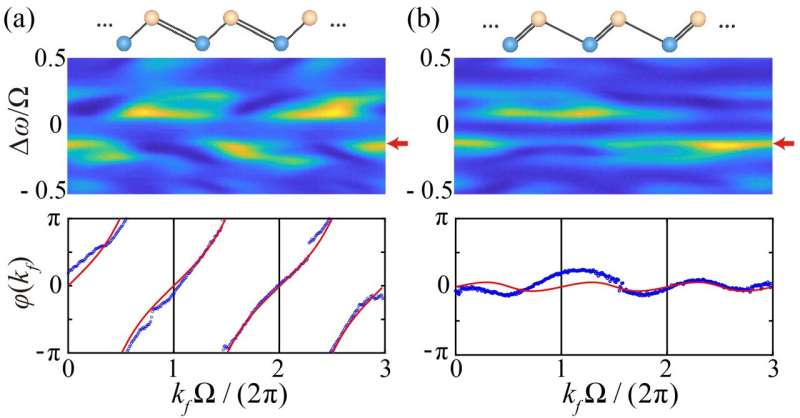
This work for the first time experimentally provides the evidence of directly reading the topological Zak phase from the distinguishable time-resolved transmission spectra in a synthetic SSH model, constructed with the frequency dimension in modulated ring resonators.

The proposed method for characterizing the topological invariant is universal in the synthetic frequency dimension and points out a new route in exploring topological phases of matter with experimental feasibility and reconfigurability. The ability of providing alternating modulations between synthetic lattice sites in experiment therefore offers new possibility to construct more complex lattice structures with nonuniform connectivities in the frequency dimension.

The topologically non-trivial and trivial transmission spectra bring possible ingredient towards exploring spectral non-reciprocity and potential applications in optical communications.