An extension of FermiNet to discover quantum phase transitions

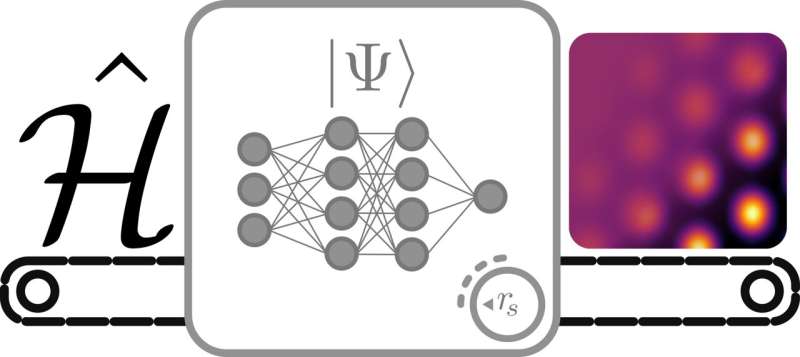
Architectures based on artificial neural networks (ANNs) have proved to be very helpful in research settings, as they can quickly analyze vast amounts of data and make accurate predictions. In 2020, Google's British AI subsidiary DeepMind used a new ANN architecture dubbed the Fermionic neural network (FermiNet) to solve the Schrodinger equation for electrons in molecules, a central problem in the field of chemistry.

The Schroedinger equation is a partial differential equation based on well-established theory of energy conservation, which can be used to derive information about the behavior of electrons and solve problems related to the properties of matter. Using FermiNet, which is a conceptually simple method, DeepMind could solve this equation in the context of chemistry, attaining very accurate results that were comparable to those obtained using highly sophisticated quantum chemistry techniques. 

Researchers at Imperial College London, DeepMind, Lancaster University, and University of Oxford recently adapted the FermiNet architecture to tackle a quantum physics problem. In their paper, published in Physical Review Letters, they specifically used FermiNet to calculate the ground states of periodic Hamiltonians and study the homogenous electron gas (HEG), a simplified quantum mechanical model of electrons interacting in solids.

"Molecules are nice, but physicists are more concerned with solving the Schrodinger equation for solid matter," Gino Cassella, one of the researchers who carried out the study, told Phys.org. "The field of 'condensed matter physics' centers around calculating the behavior of electrons in solid materials, from the wood of your desk to the silicon inside the transistors which power your phone. Naturally, then, we were curious to know if the FermiNet could yield equally accurate solutions to the Schrodinger equation for solids."

Initially, Cassella and his colleagues set out to study the HEG model. In contrast with real solids, this simplified model of solids does not contain atoms, but merely electrons that are whizzing around on a smeared-out positively charged background, which is sometimes referred to as 'jellium' (i.e., evoking the image of electrons embedded in a positively charged jelly).

"Despite its simplicity, the HEG exhibits one of the most important phenomena in the study of condensed matter physics: a quantum phase transition, known as the Wigner transition," Cassella explained. "As the density of the HEG decreases, it undergoes a transition from a 'gassy' state to a 'crystalline' state.  We wanted to solve the Schrodinger equation with the FermiNet on either side of the Wigner transition and see how accurate the solutions we obtained are compared to current state-of-the-art methods."

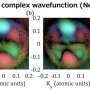
Most deep learning methods used in physics research rely on the analysis of large amounts of data, yet FermiNet does not. In contrast, it leverages the 'variational principle' of quantum mechanics, which states that the energy of a guess for the wavefunction in a given system is always equal to or greater than the energy of the so-called 'ground-state wavefunction', and only equal when a guess is exactly the same as the ground-state wavefunction.

"This ground-state wavefunction and its corresponding energy is exactly the solution we are looking for," Cassella said. "What this means is that we can use the energy as an objective function that we want to make as low as possible, this is what machine learning practitioners would call a 'loss function'. In essence, we train our neural networks guided solely by the fundamental principles of quantum mechanics."

The neural network used by the researchers is very similar to the original FermiNet, which DeepMind applied to the study of molecules. Its main difference compared to the previous version is in the way it reads the coordinates of electrons in a system, which must be modified to account for the periodic nature of the Hamiltonian. The researchers found that in addition to offering highly accurate solutions to the Schrodinger equation, FermiNet offers a unique advantage over traditional methods for studying solids.

"With existing methods to solve the Schrodinger equation, one needs to know ahead of time some of the qualitative properties of the wave function," Cassella said. "If you expect a 'gassy' wavefunction, you need to set your calculation up using functions that are 'gassy'—imagine representing the wavefunction by adding together lots of functions that are very smeared out. Likewise, if you expect a 'crystalline' wave function with lots of localized peaks, you need to set your calculation up using functions that are localized."

Writing down a wave function that is very localized as a sum of functions that are largely smeared out would require extensive computational resources and long processing times. To perform the required calculations within a reasonable time, researchers thus need to select the right functions.

"This is a problem for studying phase transitions, because now you need to change what calculation you are doing on either side of the transition," Cassella said. "Even worse, what if you don't know that a transition is even there? You might miss it completely if you choose the wrong set of functions. This is where we realized that FermiNet could come to the rescue."

In contrast with conventional calculation-based methods for solving the Schrodinger equation, neural networks do not require users to choose a set of functions. Therefore, the adapted version of FermiNet used by Cassella and his colleagues can obtain accurate solutions for the Schrodinger equation on both sides of a phase transition.

"We correctly obtain the 'gassy' state and the 'crystalline' state with exactly the same calculation, altering only the density of the HEG," Cassella explained. "This is a unique and quite amazing advantage of neural network approaches for solving the Schrodinger equation."

The recent study by this team of researchers highlights the huge potential of FermiNet as a probe for materials that undergo exotic and poorly understood phase transitions. While they so far used it to study the HEG model, it could soon also be applied to the study of phase transitions occurring in high-temperature superconductors and exotic interacting topological phases of matter.

"Our results concerning the Wigner transition are extremely promising, but what we really want to study are real materials, not simplified models," Cassella added. "Performing calculations for real materials that we can compare with experiments will require us to improve the efficiency of our calculations, so this will be a major focus for us moving forward. In the long run, we look forward to studying phase transitions in real solids!"

© 2023 Science X Network