Measuring Zak phase in room-temperature atoms
In topological insulators, global geometric phases of energy bands determine the existence of unidirectionally propagating edge states, which are immune to local defects, bringing a new stage for designing noise-resilient devices of electrons, photons and atoms. The geometric phase is measured by adiabatically transporting a quantum state through a Brillouin zone, which requires sophisticated quantum control technique. In atoms, such measurement can only be carried out at an extremely low temperature.
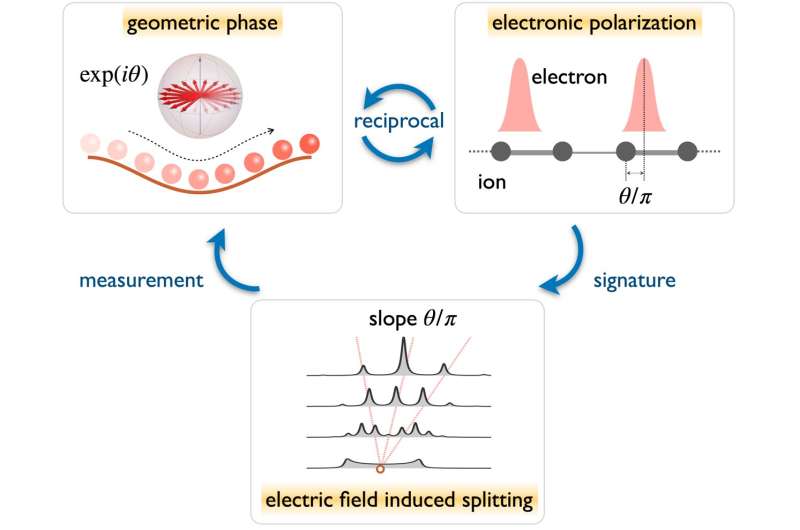
The modern theory of polarization in solids sheds new light on the measurement of geometric phases. Based on that theory, the Wannier centers (the expected positions of the Wannier functions of energy bands) are determined by the geometric phases. In a static electric field, the Wannier centers determine the energies of the Wannier-Stark ladders, from which the geometric phases can be extracted.
In a new paper published in Light: Science & Applications, a team of scientists led by Da-Wei Wang and Han Cai from Zhejiang University developed a new technique to measure geometric phases in thermal atoms. The work is implemented in superradiance lattices, i.e., momentum-space lattices of collectively excited states of atoms, the so-called timed Dicke states. The authors summarize the essence of their technique as follows.
"In momentum-space lattices, the motion of atoms plays the role of an electric field in real-space lattices. Atoms moving through the real-space Brillouin zone of superradiance lattices follow the same dynamics of lattice electrons traveling through a momentum-space Brillouin zone in a DC electric field," the scientists explained.
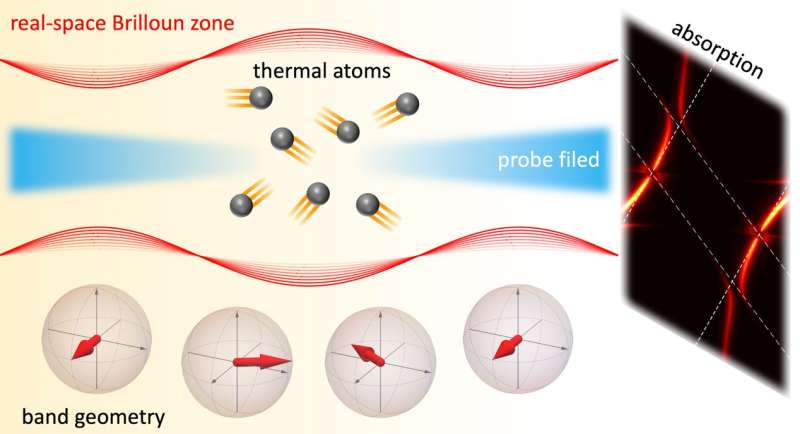
"In particular, we find that the velocity of atoms is proportional to the strengths of the effective electric field. In thermal atoms, we obtain the energy spectra of superradiance lattices by integrating Wannier-Stark spectra of atoms with different velocities. When two ladders from different energy bands have the same energy for a certain velocity, an anti-crossing happens, which is characterized by a dip in the energy spectra.
"By measuring the energies of those dips, we manage to reconstruct the geometric phases of the energy bands. The technique is applied to various one-dimensional lattices, including the Semenoff insulators, the Su-Schriefer-Heeger models, and the generalized Rice-Mele model.
"Our experiment demonstrates a conceptually novel technique in detecting band geometry of laser-dressed atoms and can be generalized to measure other topological invariants in higher-dimensional systems. Meanwhile, it also paves a way for the application of topological physics in optical devices at ambient temperature," the scientists said.
More information: Ruosong Mao et al, Measuring Zak phase in room-temperature atoms, Light: Science & Applications (2022). DOI: 10.1038/s41377-022-00990-7
Journal information: Light: Science & Applications
Provided by Chinese Academy of Sciences