Topology and machine learning reveal hidden relationship in amorphous silicon
Theoretical scientists have used topological mathematics and machine learning to identify a hidden relationship between nano-scale structures and thermal conductivity in amorphous silicon, a glassy form of the material with no repeating crystalline order.
A study describing their technique appeared in the Journal of Chemical Physics.
Amorphous solids, such as glass, obsidian, wax, and plastics, have no long-range repeating, or crystalline structure, to the atoms or molecules that they are made out of. This contrasts with crystalline solids, such as salt, most metals and rocks. As they lack long-range order in their structure, the thermal conductivity of amorphous solids can be far lower than a crystalline solid composed of the same material.
However, there can still be some medium-range order on the scale of nanometers. This medium-range order should affect the propagation and diffusion of atomic vibrations, which carry heat. The heat transport in disordered materials is of special interest to physicists due to its importance in industrial applications. The amorphous form of silicon is used in an enormous range of applications in the modern world, from solar cells to image sensors. For this reason, researchers have intensively investigated the structural signature of the medium-range order in amorphous silicon and how it relates to thermal conductivity.
"For better control over applications that make use of amorphous silicon, controlling its thermal properties is high on engineers' wish list," said Emi Minamitani, the corresponding author of the study and a theoretical molecular scientist with the Institute for Molecular Science in Okazaki, Japan. "Extracting the nano-scale structural characteristics in amorphous including medium-range order is an important key."
Unfortunately, researchers have struggled to carry out this task because it is difficult to determine the essential nano-scale features of disordered systems using traditional techniques.
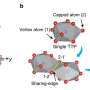
In experiments, the presence of medium-range order has been physically detected using fluctuation electron microscopy, which involves statistical analysis of scattering from nano-scale volumes of a disordered material. At the theoretical level, it has been discussed by considering the distribution of dihedral angles (the angle between two intersecting planes between sets of atoms) or using "ring statistics." The latter tries to understand the structural characteristics from the connectivity of atoms.
This in turn draws on the field of mathematics known as topology, which investigates properties of an object that do not change—or are "invariant"—even when the object is constantly stretched and deformed without being broken (such as shapes written on a rubber sheet). Focusing on this topological invariance is useful for delivering a qualitative description, such as tendency of the physical properties with respect to the randomness. However, it is demanding to determine the atomic structure corresponding to a medium-range order and predict its physical properties only from simple topological invariants.
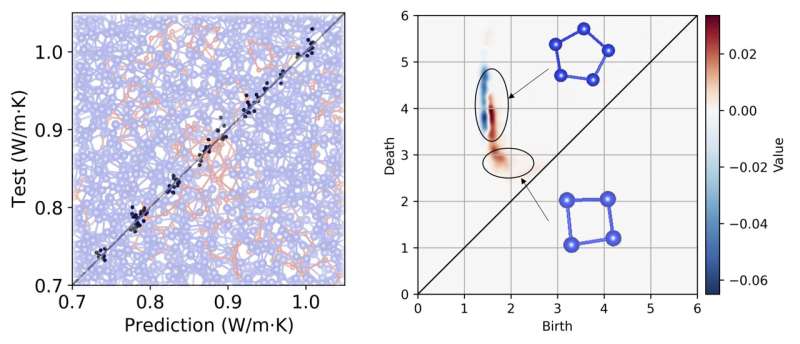
So the researchers pivoted to an emerging technique called persistent homology, a type of topological data analysis. Persistent homology has been used elsewhere to analyze complex structures ranging from proteins to amorphous solids. The benefit of this method is in detecting topological features in complicated structures at different spatial scales. This is vital because the medium-range order comprises quasi-repetitive structures at various scales. Using this characteristic, we can extract the medium-range order hidden beneath what otherwise appears as randomness.
The researchers built computational models of amorphous silicon by classical molecular dynamics wherein the temperature of the silicon was increased above the melting point and then gradually cooled (quenching) to room temperature. Differences in structural characteristics were introduced by changing the cooling rate.
Then, the persistent diagram, which is the two-dimensional visualization of persistent homology, was computed for each model. The researchers focused on that the diagrams reflect the structural features of amorphous silicon. Thus, they constructed the numerical representation, called "descriptors," that could be used in machine learning. The researcher found that the persistent diagram fulfilled the creation of a good descriptor for use in the machine learning procedure, which in turn achieved accurate predictions about the thermal conductivities.
By further analyzing the persistent homology data and machine-learning model, the researchers illustrated the previously hidden relationship between medium-range order in amorphous silicon and its thermal conductivity.
The study should now open an avenue for controlling material characteristics of amorphous silicon and other amorphous solids through the topology of their nanostructures.
More information: Emi Minamitani et al, Topological descriptor of thermal conductivity in amorphous Si, The Journal of Chemical Physics (2022). DOI: 10.1063/5.0093441
Journal information: Journal of Chemical Physics
Provided by National Institutes of Natural Sciences