New kirigami-inspired models predict how new metamaterials behave
A traditional paper crane is a feat of artistry. Every fold in origami leads to the transformation of a single square sheet of paper into a bird, a dragon, or a flower. Origami discourages gluing, marking or cutting the paper, but in the art of kirigami, strategically placed cuts can transform the shape of the paper even further, creating complex structures from simple slits. A well-known example of this is a pop-up book, where depending on how the flat paper is cut, a different set of shapes—a heart, a frog, a set of skyscrapers—will emerge when the book is opened.
In manufacturing, kirigami is changing the game of what is possible. Just like with paper, repeated laser cutting of a sheet opens up the possibility for complex shape-morphing powered by the opening and closing of slits. Because of the freedom available in designing slits, this creates a broad choice of geometries that have highly adaptable properties compared to traditional materials. In real world applications, you might see such a material used in robotics or space, for instance a snakeskin like kirigami-inspired material that allows a robot to crawl or a morphing airframe. But before these materials can be adapted for professional use, we need to better understand how kirigami materials shape-shift under typical engineering stresses and loads. While the rules for simple building blocks are known, the rules for their collective shape-shifting interactions remain largely unclear.
In a recent paper published in Physical Review Letters, a cross-disciplinary team of researchers at USC, University of Illinois at Chicago, and Stony Brook University derived a new mathematical equation for categorizing the behavior of kirigami-inspired materials to better predict how they will move when pushed or pulled. The team includes USC Assistant Professor Paul Plucinsky and Post-doctoral Fellow Yue Zheng; Stony Brook University Assistant Professor Paolo Celli and Graduate Research Assistant Imtiar Niloy; and University of Illinois-Chicago Assistant Professor Ian Tobasco.
Said Plucinsky: "The geometry of these materials is tuned somewhat arbitrarily. So we need rules about how you might choose the architectures that you're going to fabricate. Once you have those rules, you also need to be able to model the system so you make some reasonable prediction of how it will deform when pushed or pulled."
Plucinsky says previous models of material behavior do not apply to kirigami materials, as they are not sensitive to the complicated geometry of their designs. "If you want to be able to use these materials, you have to understand first why when you introduce these patterns to loads, they produce a very non-uniform response."
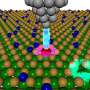
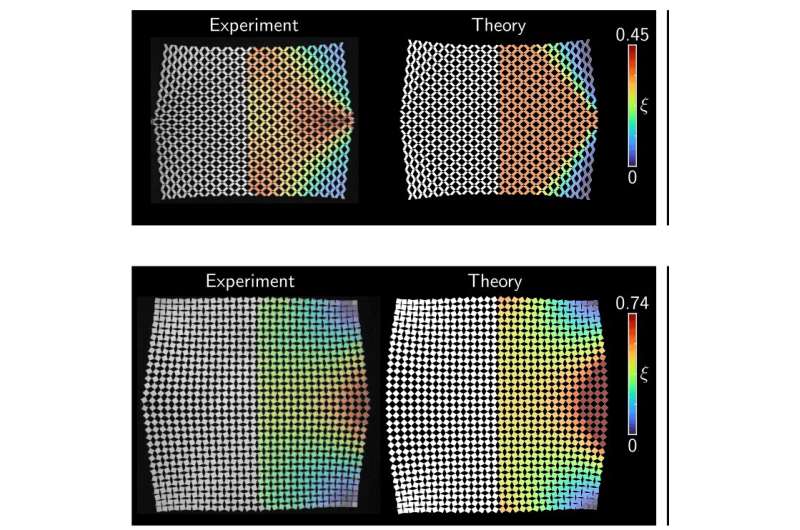
When a material is cut, it produces "cells" or contained spaces that repeat in a pattern, for instance, parallelograms, Plucinsky said. In the case of kirigami materials, these cells can be categorized to behave in one of two ways: wave-like or decaying along elliptical arcs, and this depends only on whether the pattern compresses or expands perpendicular to the pulling direction. A mathematical equation governs the geometric behavior of things like water flow, Plucinsky said, but for solids like these, it is harder to derive. A partial differential equation (PDE) is what Plucinsky and his team were able to develop and set forth as the first piece of a bigger puzzle required to make kirigami materials practically applicable.
A modeling problem
Right now, Plucinsky says while people are eager to use kirigami materials to design devices in the soft robotics, biomedical, and even space research arenas, there is a basic modeling problem that prevents their use. Plucinsky said, there's not much known about how kirigami materials function under basic loading conditions. "If you don't have a good tool to model the systems in question, you would have a hard time investigating the design space and making comprehensive predictions about the individual patterns," Plucinsky said.
In light of that, Plucinsky and his research team thought, 'is there a simple mathematical equation that could characterize these materials?" "The equation," he said, "would allow you to predict the behavior of the system in a numerically efficient way."
The key to the equation was to realize that kirigami cells, though having complicated building blocks themselves, could be conceptualized as atoms in a lattice (a repeating 2D set of atoms), like in a conventional crystalline solid, where the units are identical and repeating. From there, it was simple to derive an equation that managed to reflect the changes in the physical structure of such a material when manipulated. The equation gives insight into real-world scenarios, for instance, how a kirigami-based space object might react if a moon rock landed on it.
Puzzle pieces of design
Kirigami patterns, Plucinsky said, are beneficial for many reasons, one of which is they are material independent in many ways. "This sort of parallels nicely with additive manufacturing where they now can basically go in and at various scales create carefully engineered patterns. The point is that the pattern matters, so if you design the pattern correctly, the choice of material that you use doesn't have to matter as much."
Seeing the success of the mathematical model in predicting kirigami-inspired materials opens the doors to using such modeling for other materials, Plucinsky said. "We're working toward the idea that if you have something with a repeating pattern, you can find an equation that accurately models it. From there, we can turn this on its head so that if you want to engineer a particular property, you can say, 'oh, it needs to feature an x-type pattern,' and reverse engineer it."
More information: Yue Zheng et al, Continuum Field Theory for the Deformations of Planar Kirigami, Physical Review Letters (2022). DOI: 10.1103/PhysRevLett.128.208003
Journal information: Physical Review Letters
Provided by University of Southern California