Rational neural network advances partial differentiation equation learning
Math is the language of the physical world, and Alex Townsend sees mathematical patterns everywhere: in weather, in the way soundwaves move, and even in the spots or stripes zebra fish develop in embryos.
"Since Newton wrote down calculus, we have been deriving calculus equations called differential equations to model physical phenomena," said Townsend, associate professor of mathematics in the College of Arts and Sciences.
This way of deriving laws of calculus works, Townsend said, if you already know the physics of the system. But what about learning physical systems for which the physics remains unknown?
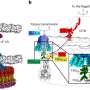
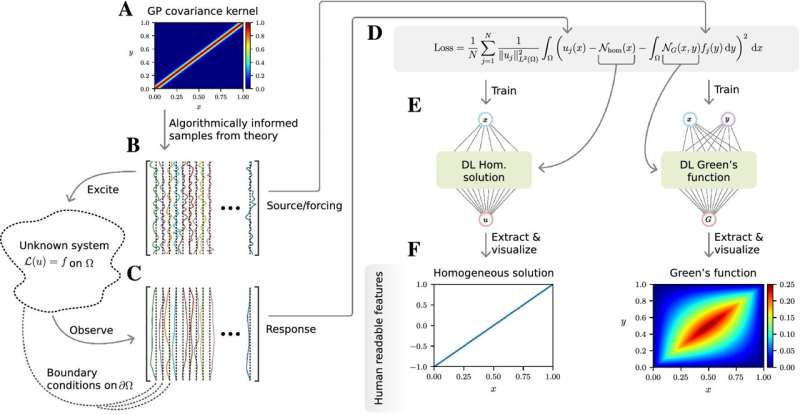
In the new and growing field of partial differential equation (PDE) learning, mathematicians collect data from natural systems and then use trained computer neural networks in order to try to derive underlying mathematical equations. In a new paper, Townsend, together with co-authors Nicolas Boullé of the University of Oxford and Christopher Earls, professor of civil and environmental engineering in the College of Engineering, advance PDE learning with a novel "rational" neural network, which reveals its findings in a manner that mathematicians can understand: through Green's functions—a right inverse of a differential equation in calculus.
This machine-human partnership is a step toward the day when deep learning will enhance scientific exploration of natural phenomena such as weather systems, climate change, fluid dynamics, genetics and more. "Data-Driven Discovery of Green's Functions With Human-Understandable Deep Learning" was published in Scientific Reports on March 22.
A subset of machine learning, neural networks are inspired by the simple animal brain mechanism of neurons and synapses—inputs and outputs, Townsend said. Neurons—called "activation functions" in the context of computerized neural networks—collect inputs from other neurons. Between the neurons are synapses, called weights, that send signals to the next neuron.
"By connecting together these activation functions and weights in combination, you can come up with very complicated maps that take inputs to outputs, just like the brain might take a signal from the eye and turn it into an idea," Townsend said. "Particularly here, we are watching a system, a PDE, and trying to get it to estimate the Green's function pattern that would predict what we are watching."
Mathematicians have been working with Green's functions for nearly 200 years, said Townsend, who is an expert on them. He usually uses a Green's function to rapidly solve a differential equation. Earls proposed using Green's functions to understand a differential equation rather than solve it, a reversal.
To do this, the researchers created a customized rational neural network, in which the activation functions are more complicated but can capture extreme physical behavior of Green's functions. Townsend and Boullé introduced rational neural networks in a separate study in 2021.
"Like neurons in the brain, there are different types of neurons from different parts of the brain. They're not all the same," Townsend said. "In a neural network, that corresponds to selecting the activation function—the input."
Rational neural networks are potentially more flexible than standard neural networks because researchers can select various inputs.
"One of the important mathematical ideas here is that we can change that activation function to something that can actually capture what we expect from a Green's function," Townsend said. "The machine learns the Green's function for a natural system. It doesn't know what it means; it can't interpret it. But we as humans can now look at the Green's function because we've learned something we can mathematically understand."
For each system, there is a different physics, Townsend said. He is excited about this research because it puts his expertise in Green's functions to work in a modern direction with new applications.
More information: Nicolas Boullé et al, Data-driven discovery of Green's functions with human-understandable deep learning, Scientific Reports (2022). DOI: 10.1038/s41598-022-08745-5
Journal information: Scientific Reports
Provided by Cornell University