Identifying a topological fingerprint

A FLEET theoretical study out this week has found a 'smoking gun' in the long search for the topological magnetic monopole referred to as the Berry curvature.

This discovery is a breakthrough in the search for topological effects in non-equilibrium systems .

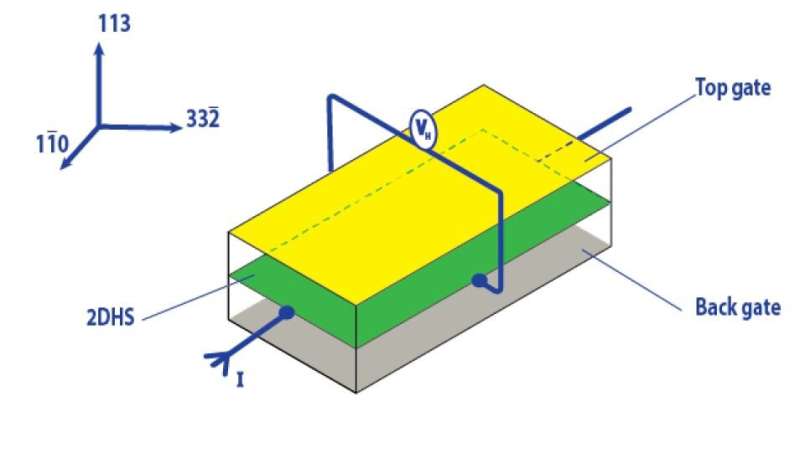
The group, led by Dimi Culcer at UNSW, identified an unconventional Hall effect driven by an in-plane magnetic field in semiconductor hole systems, which is traced exclusively to the Berry curvature.

(Conversely, the ordinary Hall effect and anomalous Hall effect both require a magnetic field/magnetisation that is perpendicular to the surface.)

Enhanced topological effects would permit low-energy topological electronics viable for large-scale, room-temperature operation, and were recently included in the IEEE roadmap towards future electronics.

Isolating response a breakthrough moment

"Isolating topological responses in 'regular conductors' has been a historically difficult task," says research team leader A/Prof Dimi Culcer (UNSW). "Even though these topological responses are believed to be ubiquitous in solids."

Quantized responses, such as the quantum Hall and quantum spin-Hall effects provide a clear fingerprint of topology, yet these have only been observed in one-dimensional (1D) systems and are intimately connected with the existence of edge states.

In `regular' conductors, meaning 2D and 3D systems, plenty of theoretical literature exists predicting topological contributions to e.g. the anomalous Hall effect, but these have never been observed unambiguously in a transport measurement.

There are two main reasons for this: (i) spin-up and spin-down electrons usually make opposite contributions, and these nearly cancel out; (ii) whatever is left is overwhelmed by disorder.

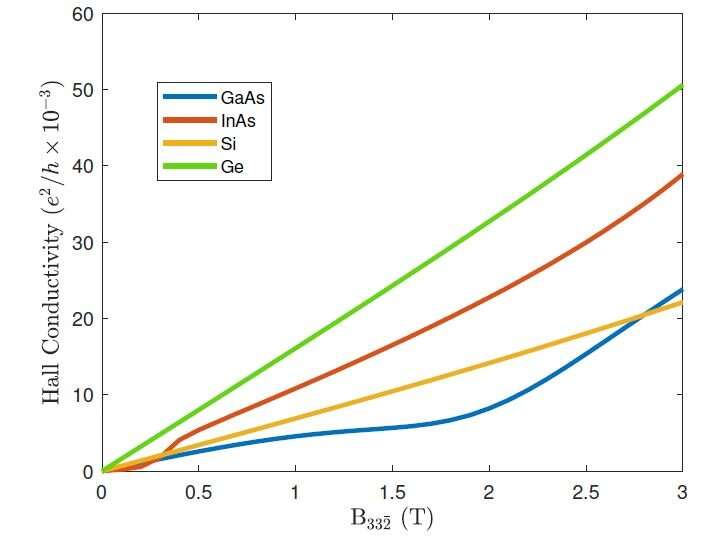
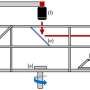
The new FLEET paper remedies this long-standing shortcoming by identifying a two-dimensional system in which the Berry curvature, and only the Berry curvature, is responsible for the Hall signal linear in the applied in-plane magnetic field.

"Remarkably, all disorder contributions vanish: we are not aware of any other multi-dimensional system in which this is true," says lead author, UNSW Ph.D. student James Cullen. "Its experimental measurement is accessible to any state-of-the-art laboratory worldwide, hence we expect strong interest from experimentalists."

Berry curvature, the anomalous Hall effect and topological materials

The research team sought the tell-tale mathematical trace called "Berry curvature," which can be understood if we think of the concept of parallel transport that appears routinely in geometry and general relativity.

"Think of a vector as an arrow that we place somewhere on the surface of a solid object," explains Dimi. "Now we move the arrow around, making sure it always points at the same angle to the surface—this is in fact like a human being walking along the surface of the Earth. We eventually bring the arrow back to the starting point after it has circled around, and we find that, in general, it points in a different direction—it has magically rotated through some angle. The size of this angle is determined by the curvature of the surface. "

In quantum mechanics, instead of vectors we have wave functions, but we can describe the dynamics using the same picture, and the curvature is called the Berry curvature.

The angle of rotation is replaced by the famous Berry phase, named after the mathematical physicist Prof Sir Michael Berry, who formulated the problem in the 1980s. Later on, building on work by Nobel laureate David Thouless, Qian Niu of UT Austin showed that the Berry curvature behaves like the coveted magnetic monopole—but not in real space, rather in momentum space, which is the space most condensed-matter physicists think in.

The Berry curvature drives topological effects in out-of-equilibrium systems because when an electric field is applied an electron is accelerated, so its momentum changes. When this happens its wave function changes slowly, in the same way that the `arrow' is rotated in parallel transport, and as a result of this gradual rotation a transverse (Hall) current is generated. The Onsager relations, which are fundamental to non-equilibrium physics, say that the Hall current does not dissipate energy. The extreme case is the quantum anomalous Hall effect (QAHE), a quantum effect key to the function of topological materials, in which edge currents can flow with effectively zero electrical resistance.

('Quantum' describes 'step' transition in the transverse (Hall) resistance—i.e., it varies in discrete steps rather than smoothly—while 'anomalous' refers to the phenomenon's occurrence in the absence of any applied magnetic field.)

Researchers seek to enhance QAHE in order to protect topological behavior at higher temperatures, allowing for topological electronics that would be viable for room-temperature operation.

"The significant reduction in electrical resistance permitted by room temperature QAHE would allow us to significantly reduce the power consumption in electronic devices," says Dimi.