June 24, 2021 feature
Observing a prethermal discrete time crystal
A framework of statistical physics can be extended to the nonequilibrium setting to discover previously unidentified phases of matter catalyzed by periodic driving. Scientists aim to reduce the runaway heating associated with driving a strongly interacting quantum system in order to investigate newly discovered phases.
In a new study now published on Science, A. Kyprianidis and an interdisciplinary research team in the U.S. used a quantum simulator to observe signatures of a nonequilibrium driven phase without disorder to form a prethermal discrete time crystal. The scientists overcame the heating problem by using high-frequency driving to form an expansive time window for nonequilibrium phases to emerge. The team presented Floquet prethermalization as a general strategy to create, stabilize and study intrinsically out-of-equilibrium phases of matter.
Periodic driving
Periodic driving or modulation of a system is a versatile method that allows the emergence of phenomena ranging from parametric synchronization to dynamic stabilization. The method is stable and staple in fields from nuclear magnetic resonance spectroscopy to quantum information processing. On a more fundamental level, the periodic Floquet drive also provides a system with a discrete time-translational symmetry, where the symmetry can be used to protect newly discovered Floquet topological phases or form time-crystalline order.
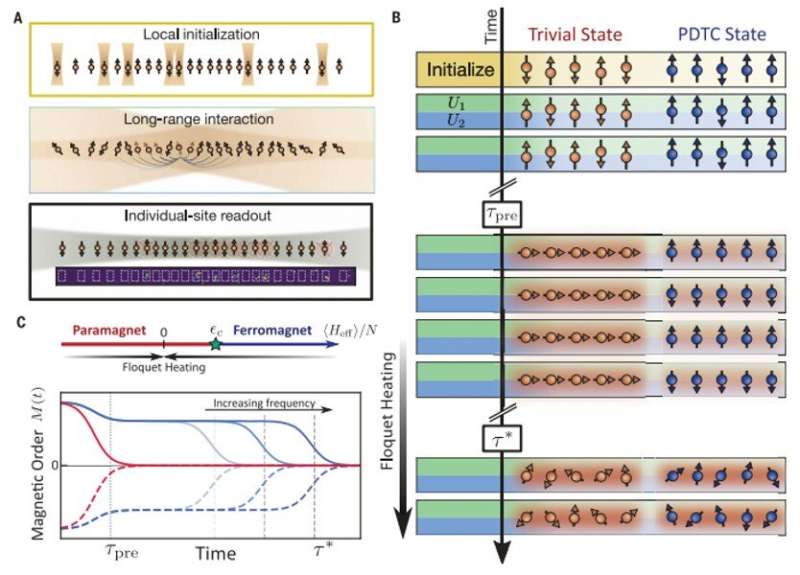
To realize many-body Floquet phases of matter, scientists must ensure that the surrounding system does not absorb energy from the driving field. In the presence of a periodic drive, Floquet heating can cause a generic many-body system to approach nontrivial order, which is followed by characterizing a phase of matter to form steady-state behavior. Conventionally, scientists can address the process to prevent Floquet heating by making use of the strong disorder in the experimental setup, in another method, they can use a disorder-free framework to address these challenges through Floquet pre-thermalization. Additional symmetries that are protected by the discrete time-translational symmetry of the drive can emerge and lead to intrinsically non-equilibrium phases of matter. An example of one such phase is the pre-thermal discrete time crystal (PDTC) where the many-body system can lead to the development of a robust subharmonic response. As a result, a disorder-free prethermal discrete time crystal showed a number of discrete key differences when compared with the many-body system discrete time crystal.
![Characterizing the prethermal regime. (A and B) The dynamics of the energy density for a low-energy Néel state (A) and a high-energy polarized state (B) highlights the frequency dependence of the heating rate. Statistical error bars are of similar size as the point markers. (C) Heating time for the Néel (red) and polarized (blue) states, extracted through an exponential fit to the energy density dynamics [solid curves in (A) and (B)]. The presence of external noise leads to a saturation of heating time at high frequencies. Error bars for the heating time correspond to fit errors. (D) Characterization of the prethermal equilibration time, via the local magnetization dynamics for even Floquet periods. (Top) The middle two spins (purple), initially prepared along the z axis, rapidly align with their neighbors (orange) signaling local equilibration to the prethermal state. The shaded bands represent the standard error of the mean. (Bottom) magnetization dynamics across the entire ion chain. Credit: Science, doi: 10.1126/science.abg8102 Observing a prethermal discrete time crystal](https://scx1.b-cdn.net/csz/news/800a/2021/observing-a-prethermal-1.jpg)
Exploring the prethermal discrete time crystal
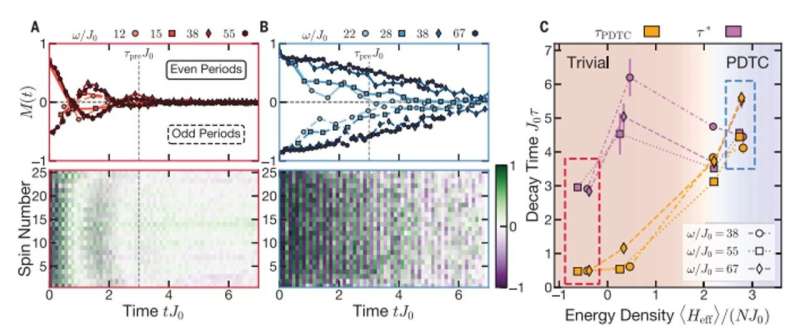
Kyprianidis et al. explored the long-range spin-spin interactions of a quantum simulator to observe the signatures of a one-dimensional prethermal discrete time crystal. The scientists first prepared a variety of locally inhomogeneous initial states by individually addressing ions within the one-dimensional chain. They then characterized the quench dynamics starting from these states to directly observe the approach to the prethermal state for the experimental extraction of the prethermal equilibration time. The team also measured the time dynamics of the energy density as a function of the driving frequency and prepared states near the bottom and top of the spectrum to observe the energy dynamics of the experimental setup. The heating time-scale increased with the driving frequency and the team investigated the nature of the prethermal time-crystalline order by studying the Floquet dynamics of different initial states of equilibrium and symmetry. During further experiments, Kyprianidis et al. identified the phase boundary for the PDTC (pre-thermal discrete time crystal) by observing the lifetime of the time-crystalline order as a function of the energy density of the initial state.
Time-crystalline order
In the experimental setup, a crucial feature of the effective prethermal Hamiltonian (Heff) of the system ensured long-range Ising interactions to stabilize a ferromagnetic phase. Due to the antiferromagnetic nature of the interactions, the phase did not occur at low energy density close to the bottom of the spectrum but occurred at high energy density near the top of the spectrum. The scientists showed the frequency dependence of the heating time-scale and the ability to determine the lifetime of the prethermal time-crystal. The key ingredient underlying the time-crystalline order was the presence of an emergent symmetry as a direct consequence of the periodic driving protocol. During the experiment, the symmetry corresponded to a global spin flip, to suggest that time-crystalline order is naturally facilitated by the magnetization dynamics of the experimental setup. As a result, there are two possibilities for the pre-thermal dynamics depending on the energy density of the system. For instance, if the prethermal state corresponded to the symmetry-respecting paramagnet, the magnetization can remain unchanged across a period. If the prethermal state corresponded to a different ferromagnet, the magnetization can alternate. The resulting subharmonic dynamics form the hallmark of a time crystal. The researchers investigated the two regimes by measuring the autocorrelation of magnetization. By considering two additional initial states, they explored the stability of the PDTC phase as a function of energy density.
Outlook
In this way, Kyprianidis et al. described both the heating time and lifetime of the time-crystalline order. The results are consistent with a phase boundary occurring at energy density in agreement with numerical calculations from quantum Monte Carlo. The team described the experimental observation of robust prethermal time-crystalline behavior that persisted beyond early-time transient dynamics. Even in the presence of noise, the pre-thermal dynamics remained stable to suggest that an external bath at sufficiently low temperatures can stabilize the prethermal dynamics for infinitely long times. This is in contrast to localization-based approaches used to stabilize Floquet phases. The outcomes of this research point to a number of future directions, including exploring the generalization of Floquet prethermalization, stabilizing Floquet topological phases and leveraging non-equilibrium many-body dynamics for metrology.
More information: Kyprianidis A. et al. Observation of a prethermal discrete time crystal, Science, 10.1126/science.abg8102
Zhou H. et al. Quantum Metrology with Strongly Interacting Spin Systems, Physical Review X, doi.org/10.1103/PhysRevX.10.031003
Peng P. et al. Floquet prethermalization in dipolar spin chains, Nature Physics, doi.org/10.1038/s41567-020-01120-z
Journal information: Science , Nature Physics , Physical Review X
© 2021 Science X Network