Researchers use optical data to reveal the basic structure of spacetime in rotating frames

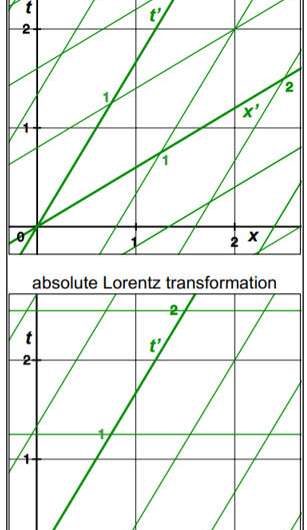
One of the most basic structural aspects of relativistic spacetime is the description of how time and distances are altered by motion. The theory of special relativity describes a spacetime framework for linear constant motion in which time dilates and lengths contract in response to motion. This framework is described by the Lorentz transformation, which encompasses mathematical formulas that describe how time and distance are altered between moving reference frames. The Lorentz transformation also describes how a stationary observer views time in the moving frame to be offset with distance. The offsetting of time with distance between reference frames generates differential simultaneity, in which events that are simultaneous for one observer will not be simultaneous for a second observer moving relative to the first observer.

The nature of spacetime in rotating frames has not been established at the most fundamental level of defining the transformation that accurately describes the relativistic effects and the simultaneity framework. There are four distinct rotational relativistic transformations in the literature: the Langevin metric; Post transformation; Franklin transformation; and the absolute Lorentz transformation (ALT) in its rotational form. Determining which transformation accurately describes experimental data would indicate the spacetime framework that is present in real-world rotating frames. Understanding this fundamental information has wide applicability because the majority of visible matter in the Universe is in rotational motion, including the rotating Earth.

The most widely-cited rotational transformation is the Langevin metric, which was first described in 1921. Over the decades, the Langevin metric has been used to describe relativity in rotating frames in hundreds of textbooks and research papers. However, the Langevin metric has never been assessed with experimental data that has sufficient resolution to distinguish it from the other major rotational transformations.

A transformation's combination of relativistic effects and simultaneity framework affects how light propagates. The four transformations have different predictions for the rotating-frame one-way speeds of light, two-way speed of light, and the Sagnac effect. This study derives the optical predictions for each transformation directly from their transformation equations, with several of the predictions not previously reported in the literature. The predictions are then compared to recent high-resolution optical experimental data.

Optical resonator data on the two-way speed of light is among the highest resolution scientific measurements, with resolutions of 10^-18. This high resolution is required to distinguish between the predictions of the transformations. The study reveals that ALT and the Franklin transformation prediction of the constant two-way speed of light, c, matches the optical resonator data, while the Langevin metric and Post transformation predictions are invalidated by the data. The failure of the Langevin metric and Post transformation to match optical resonator data is shown to be due to their exhibiting no (or no net) length contraction in the rotating frame. In contrast, the ALT and Franklin transformations exhibit length contraction, which allows their accurate predictions for the two-way speed of light.

Data on the Sagnac effect, which has lower resolutions of 10^-8, is compatible with the Sagnac effect predictions of the Langevin metric, Post, and ALT transformations, but is incompatible with the Franklin transformation, which predicts no Sagnac effect. The failure of the Franklin transformation to generate an overt Sagnac effect is shown to be due to its incorporation of differential simultaneity. In contrast, the other three transformations incorporate absolute simultaneity in which time is not offset with distance, which allows overt Sagnac effects. Thus, ALT is the only transformation that accurately describes the full range of relativistic optical data.

Multiple publications have proposed mechanisms to incorporate differential simultaneity into rotating frames to allow the generation of an overt Sagnac effect. However, these mechanisms generate alternate Sagnac effect equations. The study shows that these alternate Sagnac effect equations imply two-way speeds of light that are invalidated by the high-resolution optical resonator data. In contrast, ALT predicts the conventional Sagnac effect, which implies the constant two-way speed of light, c.

The study demonstrates that the ALT rotational transformation accurately predicts both high-resolution optical data and non-optical rotating-frame relativistic observations. This analysis implies that the ALT rotational transformation describes the basic framework of spacetime in rotating frames. This clarifies that rotating-frame spacetime is characterized by the relativistic effects of time dilation and length contraction within an absolute simultaneity framework in which time is not offset with distance.