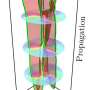
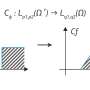
Tracking the evolution of Maxwell knots
Maxwell equations govern the evolution of electromagnetic fields with light being a particular solution of these equations in spaces devoid of electric charge. A new study published in EPJ C by Alexi Morozov and Nikita Tselousov, from the Moscow Institute of Physics and Technology and the Institute of Transmission Problems, Russia, respectively, details peculiar solutions to the Maxwell equations—so-called Maxwell knots. The research could have applications in the fields of mathematical physics and string theory.
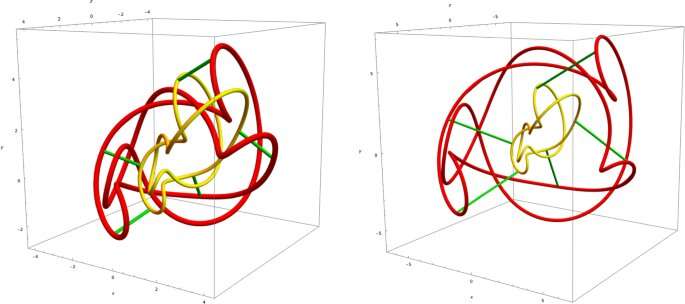
"We usually think of light as the plane waves. It was a breakthrough when 'knotted' light solutions were discovered," explains Tselousov. "The knot nature of these solution consists in the structure of the electric and magnetic field lines. One can observe that some of the field lines are closed loops and non-trivially knotted."
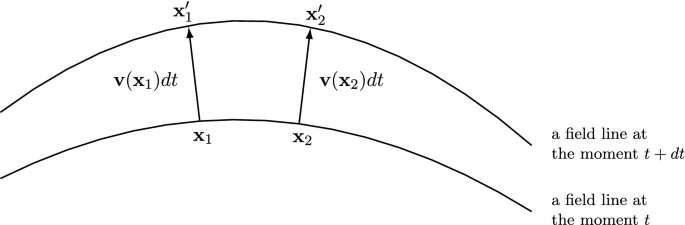
Electric and magnetic field lines change over time obeying the Maxwell equations. As the fields change their field lines somehow move in the space. Whilst researchers can't track an arbitrary field line, closed field lines are special and can be observed as they evolve over time.
"In our paper, we make a conjecture, that knotted field lines move in a very special manner in which the knotted structure remains," Tselousov continues. "In other words, one can say that this time evolution never involves self-crossings or crossings of two field lines."
Tselousov believes that should this conjecture—arrived at with the use of complex computer simulations—be correct, the conservation of the knots implies that their evolution is integrable—capable of undergoing the mathematical function integration. This means that its evolution can be related to other models and systems—in particular with non-linear equations—that are known to share this property.
"It is very rare and always a pleasure to observe the integrable properties of systems because it means deeper understanding and possible further progress. We plan to move in this direction and find more connections with integrability," Tselousov concludes. "In my mind, one of the stunning facts is that light, so familiar to everyone, conceal secrets that we used to ignore for centuries."
More information: A. Morozov et al. Are Maxwell knots integrable?, The European Physical Journal C (2020). DOI: 10.1140/epjc/s10052-020-08745-7
Provided by SciencePOD