Mathematicians create a method for studying the properties of porous materials

Mathematicians from RUDN University have studied the properties of compositional operators in spaces with mixed Lebesgue norms. Their work will help describe the diffusion of liquids in materials with cracks and in porous materials. Such spaces are also useful for obtaining estimates for solutions to the Navier-Stokes equation. The article was published in Mathematical Notes.

The modern science of partial differential equations has its own theory: the language of functional analysis. Studies of function spaces in which solutions to equations are sought began in the 19th century and have continued to the present. At first, mathematicians learned to apply Fourier theory to solutions for the simplest linear partial differential equations, then studied Banach and Hilbert spaces, as well as spaces of generalized functions, which is essentially the language of quantum mechanics.

Around the middle of the 20th century, Sobolev spaces were discovered; these now occupy one of the central positions in the theory of partial differential equations. Over the next 50 years, they helped mathematicians find many solutions to applied problems that cannot be found in ordinary functional spaces.

Closer to the beginning of the 21st century, it became necessary to find new methods to study nonlinear partial differential equations, so computational mathematics and the theory of integrable systems were developed. However, methods from these fields turned out to be too narrowly focused, and the need to develop the language is still there.

Lebesgue spaces with mixed norms are sometimes more universal and flexible objects. These spaces are determined as follows: In the space of functions in several variables, define the norm by iterating Lebesgue norm. They initially arose as one of the generalizations of Sobolev spaces and have already attracted a lot of interest from theorists from several countries of Europe, as well as China, Canada and Russia.

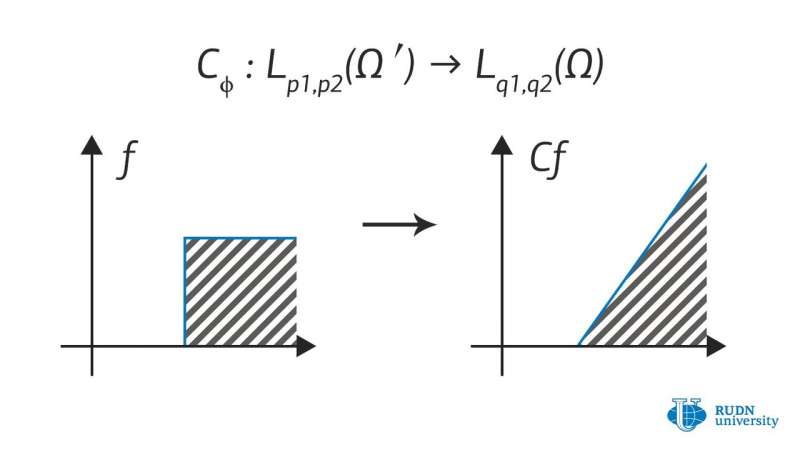
Nikita Evseev and Alexander Menovshchikov from the Mathematical Institute of RUDN University work on a theory of operators for such spaces, which allows their use in applied problems formulated in the language of partial differential equations. They produced quite a number of new results describing the properties of operators on such spaces: criteria for boundedness of operators, properties of integral operators, multiplication operators, composition operators, and many others. They also obtained a few auxiliary results useful for the further development of this field.

"Our methods and results, we believe, can be applied to evolutionary problems and differential problems on non-cylindrical regions. For example, in (mathematical) biology, where the surface or the area under study changes with time, or in hydrodynamics, for problems with a variable boundary," says Evseev.

Research in this field is useful for studying the Navier-Stokes equations, a system of equations describing aero- and hydrodynamics. Lebesgue spaces with mixed norms make it possible to evaluate solutions, which, in turn, allows predicting an absence of turbulence, for example.

The results will also help study the applied problems of mathematical physics arising in the study of porous materials and materials with cracks. For example, it will be possible to theoretically predict the pattern of diffusion and heat transfer in silica gels, porous glasses, various sponges, and foams, as well as in some building materials.